Introduction to Electronic Devices
对应的 Github 仓库地址是:
https://github.com/Cateds/ElectronicDevice.md
有帮助的话记得点个 Star 支持一下。
如果能开一个 Pull Request 来补充内容就更好了。
Block 1: Semiconductor Fundamentals
Lec.1 General Material Concept
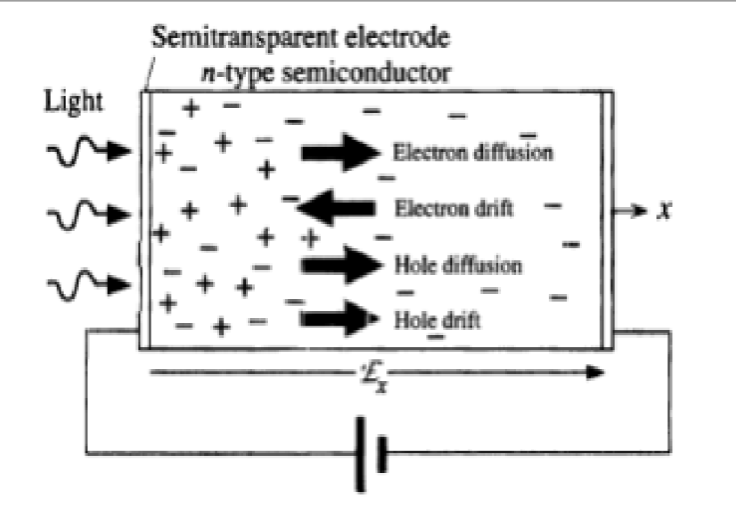
半导体的晶体特性和发展
半导体是一类电导率在金属和非金属之间的材料。电导率 (Electrical conductivity) 指的是一种物质传导电流的能力,和电阻紧密相关:,其中 是电导率,单位是, 是电阻率 (Electrical resistivity),单位是。
对于一个电阻,有欧姆定律 ,代换后有
常见的半导体有两种,一种是 元素半导体 (Elemental Semiconductors) ,如硅 (Si) 和锗 (Ge),因为他们由单一种类原子组成;另一种是 化合物半导体 (Compound Semiconductors),如砷化镓 (GaAs) 和氮化镓 (GaN)。
半导体和其他材料最大的区别在于它的能带间隙,即 禁带宽度 (Band gap),它决定了材料的导电性能。为了研究半导体的特性,有必要了解材料中的原子排列。
晶格 (Crystal Lattice) 是指材料中原子的周期性排列。晶体的独特之处,就是它的周期性排列。晶体的周期性是在空间中以对称排列的点阵来定义的,在每个点阵点上添加原子,形成一种叫做基元 (basis) 的排列。
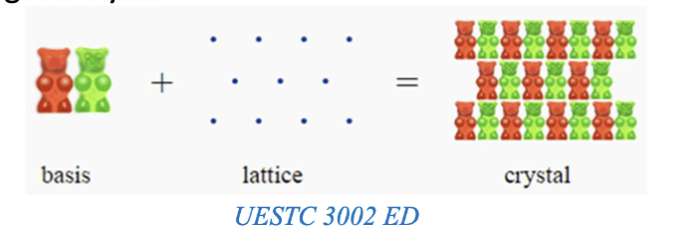
由于在一定的体积里放置原子的方式有很多种,原子之间的距离和方向有多种形式,所以可能会产生不同的晶格和晶体结构。比如简单堆积 (Simple Cubic, SC)、体心立方 (Body-Centered Cubic, BCC)、面心立方 (Face-Centered Cubic, FCC) 等等。
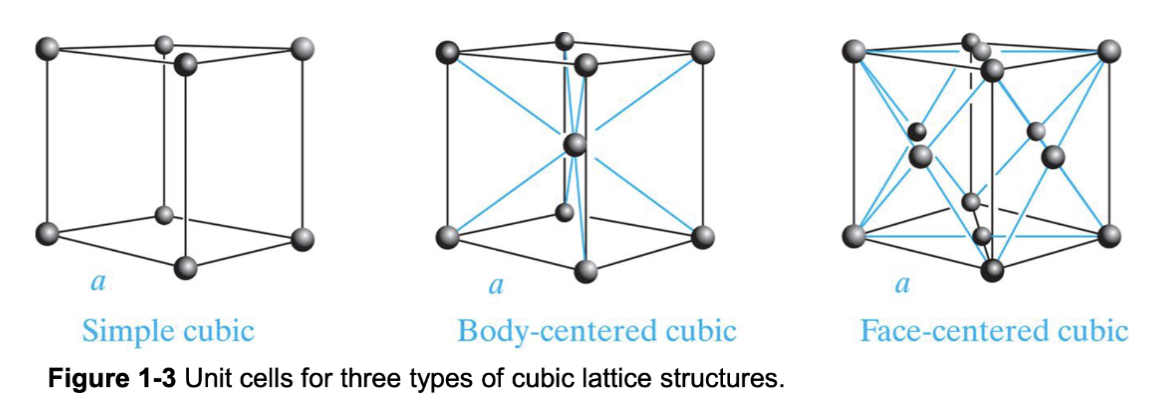
原子被填充在点阵中时,相互之间会有力相互吸引以及相互排斥,最终稳定的状态是二者相互平衡。这里可以将原子近似为一个球体来计算。在这种情况下,可以计算出一个晶格体积下可以填充的原子体积。一个晶格的边长被称为 晶格常数 (Lattice Constance),用 表示。对于不同的晶格结构,可以计算出填充因子 (Packing Factor)
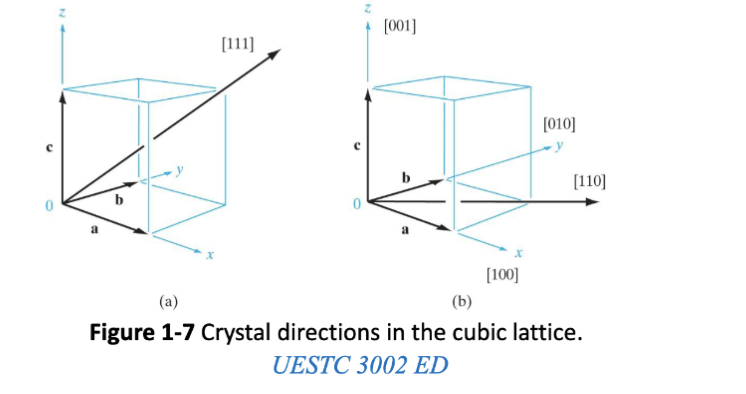
在讨论晶体时,一个很重要的方向是获得点阵内的平面和方向。这种符号系统使用三个整数来描述点阵哪平面和向量的位置:
- 找到平面与晶轴的截距,并将这些截距表示为基向量的整数倍(可以将平面沿其方向移入移出原点,直到在每个轴上都发现整数截距)
- 取步骤 1 中找到的三个整数的倒数,并将它们简化为最小的整数集合 ,这些整数彼此之间具有与三个倒数相同的关系
- 标记该平面为
在空间直角坐标系中,这三个数字实际上组成的就是这个面的法向量。
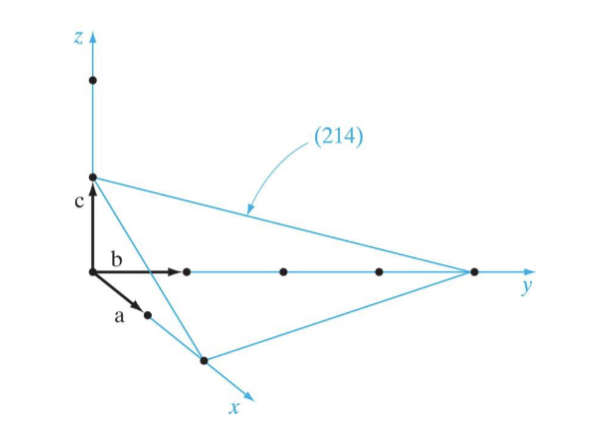
晶格中的方向同样用三个整数表示。各个方向的向量方向是对应边的方向,且长度和对应的边相同,以这三个向量作为基底建立坐标系。这样,每个方向都可以以从原点指向某个坐标的向量决定,记作 。等效的方向用尖括号表示 ,比如对于立方晶格,相邻边垂直相等, 是等效的,记作
许多重要的半导体的基本晶体结构是剧有两原子基的面心立方点阵,进而产生金刚石结构————比如 Si, Ge, 以及金刚石形态的 C。描述金刚石结构的简单方式是吧金刚石结构看作一个面心立方点阵,在每一个面心立方原子处放置一个额外的原子,对应的位置是
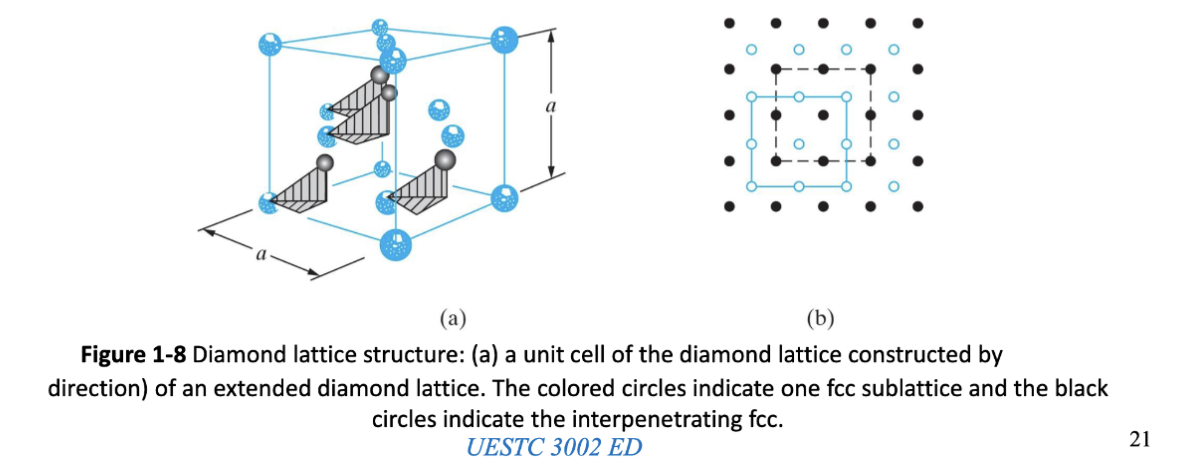
晶格和晶胞
原子堆积因子 (Atomic Packing Factor, APF) 的定义是一定体积内被原子占据的体积与该体积的比值。APF 可以用来描述晶体中原子的紧密程度。对于不同的晶体结构,APF 的值是不同的。
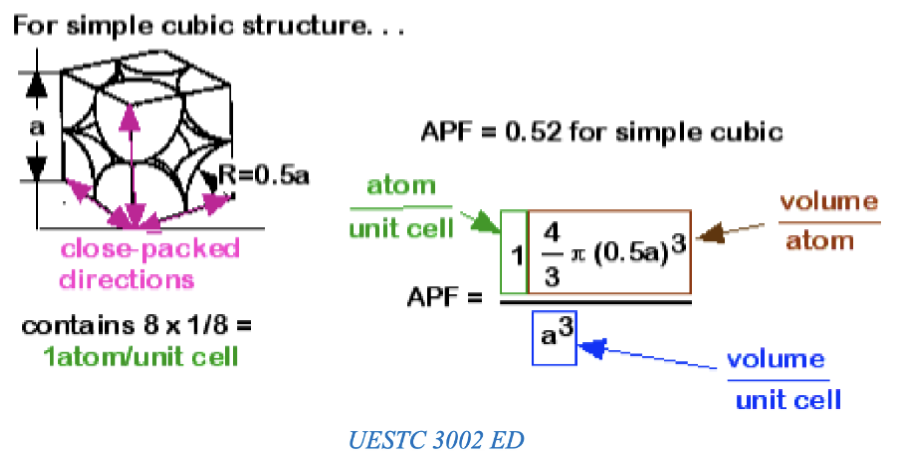
对于体心立方堆积 (BCC),根据原子是硬球体的等效,其在对角线上接触紧密,故有 ,其中 是原子的半径,进而计算出 APF。
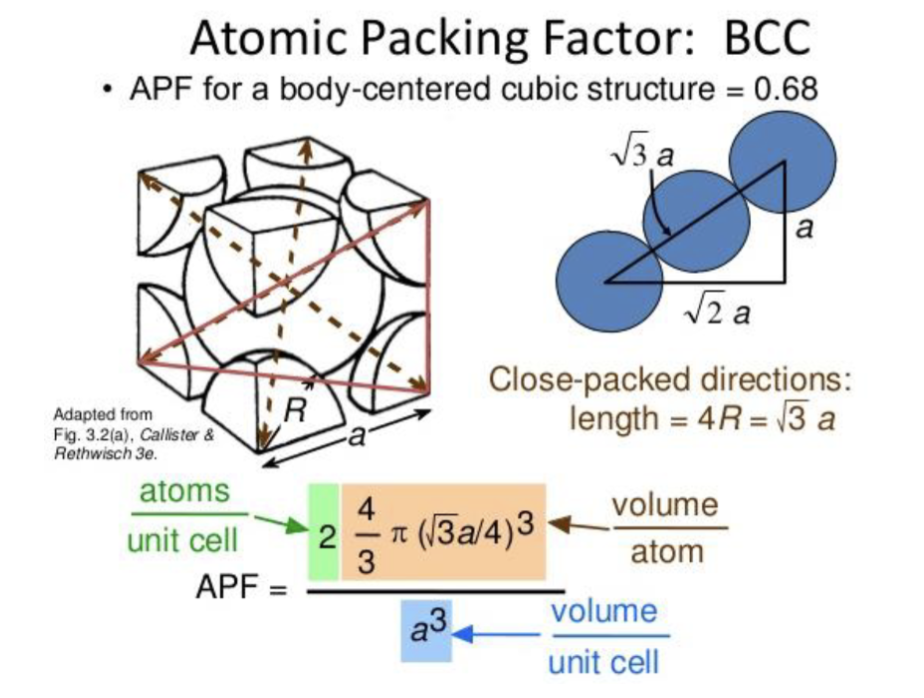
对于面心立方堆积 (FCC),则是在面对角线上紧密接触,有 ,其中 是原子的半径。
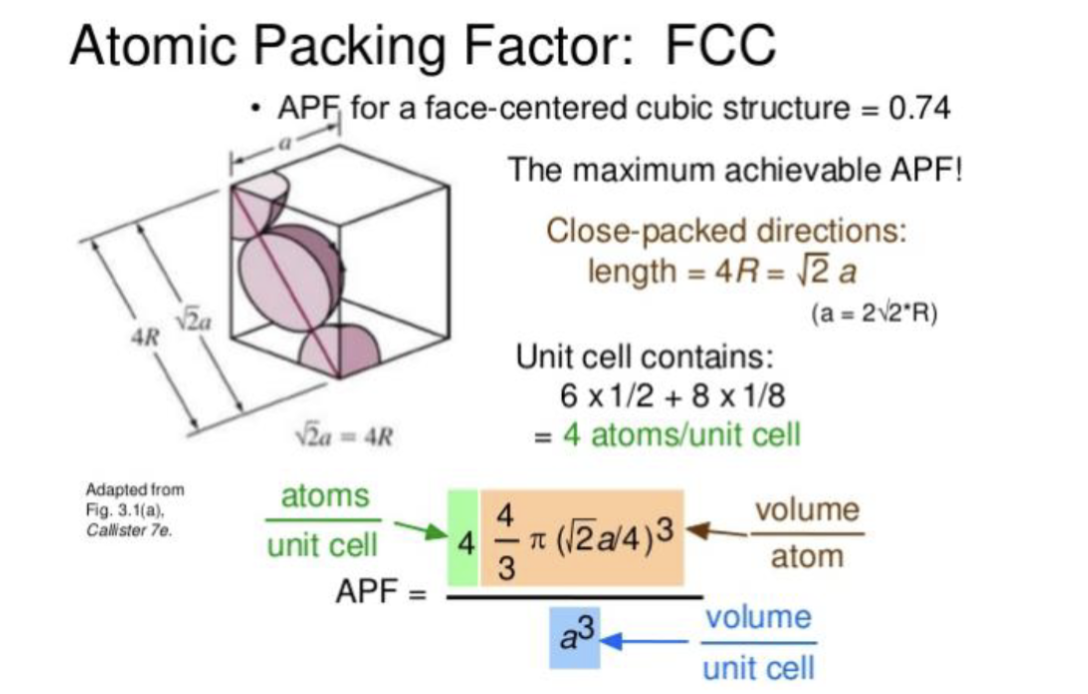
晶体生长
固态器件技术的发展不仅取决于器件概念的进步,还取决于材料的改进。例如,如今能够制造集成电路的事实,是 20 世纪 50 年代早期和中期在纯单晶硅生⻓方面取得重大突破的结果。对器件级半导体晶体生⻓的要求比任何其他材料都更为严格。不仅半导体必须以大单晶形式存在,而且纯度必须控制在极其严格的范围内。例如,用于设备的 Si 晶体在生⻓过程中,大多数杂质的浓度低于十亿分之一。这种纯度要求 在制造过程中对材料进行仔细的处理和操作。Si 晶体的原料是二氧化硅(SiO₂)。SiO₂ 在高温炉(~1800°C)中与 C 反应,根据以下反应式还原 SiO₂:
这形成了冶金级别的硅单质 (Metallurgical Grade Si, MGS),其中含有 2ppm (Parts per million) 级别的杂质,还需要进一步提纯得到半导体级别或电子级硅 (Electronic-Grade Si, EGS),杂质降低到 ppb (Parts per billion) 级别
下一步是把高纯度但是仍然是多晶的 EGS 硅转化成单晶硅 (ingots),这一步使用的方法叫做柴可拉斯基法 (Czochralski Method)。
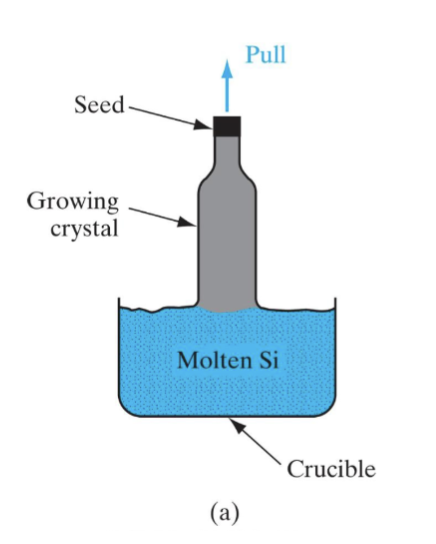
这个过程首先需要一个籽晶 (Seed Crystal),把它下降到熔融的硅中,然后缓慢提起,让晶体在籽晶上生长,进而产生大块单晶硅。之后,在产生的单晶硅上进行操作,生产出晶圆以及芯片。

原子和电子
光电效应 (Photoelectric Effect) 是指当光照射到某些材料表面时,材料会释放电子的现象。这个现象最早由爱因斯坦在 1905 年解释,他提出光具有粒子性,光子 (Photon) 的能量与其频率成正比,公式为 ,其中 是普朗克常数, 是光的频率。普朗克指出,辐射是以离散的能量单位发射的,成为 量子 (Quantum)。

光电效应是一个重要的量子现象,它让我们能够清晰的理解光和电子的量子性质。这一效应说明光表现为被称为光子的离子,每个光子携带特定的能量。
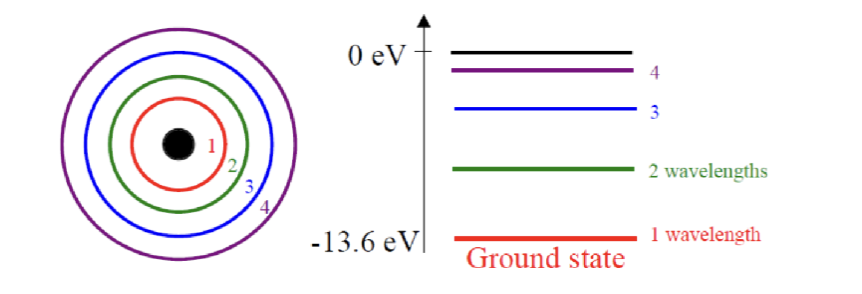
我们用来理解原子的原子模型一般是一个简化的模型,被称为壳层模型 (Shell Model),基于玻尔模型。电子在固定半径的离散量子化轨道上绕原子核运行;电子可以被视为包含在一个特定半径内的球形壳内的电荷;电子可以通过失去或吸收能量从一个轨道跃迁到另一个轨道。
原子的质量集中在原子核 (nudeus) 上,原子核由质子和中子组成。质子带正电,中子不带电。电子带负电,质量远小于质子和中子。中子和质子的质量大致相同。原子核中的质子数就是元素的原子序数。电子数等于质子数,因此原子整体上是电中性的。
电子被认为在原子核外非常大的距离绕核运动。电子的位置主要由两组整数标记:主量子数 和角量子数 。主量子数 决定电子的能量和电子云的大小, 的值为正整数 (1, 2, 3, …)。角量子数 决定电子云的形状, 的值为非负整数 (0, 1, 2, …, n-1)。每个 和 对应一个电子壳 (shell) 和亚壳 (subshell)。每个亚壳可以容纳一定数量的电子,具体数量由 给出。对于 的壳分别标记为 K, L, M, N, …,对于 的亚壳分别标记为 s, p, d, f, …
对于一个亚层,电子的自旋 (spin) 量子数 可以取两个值:+1/2 或 -1/2。根据泡利不相容原理 (Pauli Exclusion Principle),每个亚层最多可以容纳 个电子。当一个亚层被填满后,它不再能容纳更多电子,此时它被认为是稳定的 (stable)。
能带
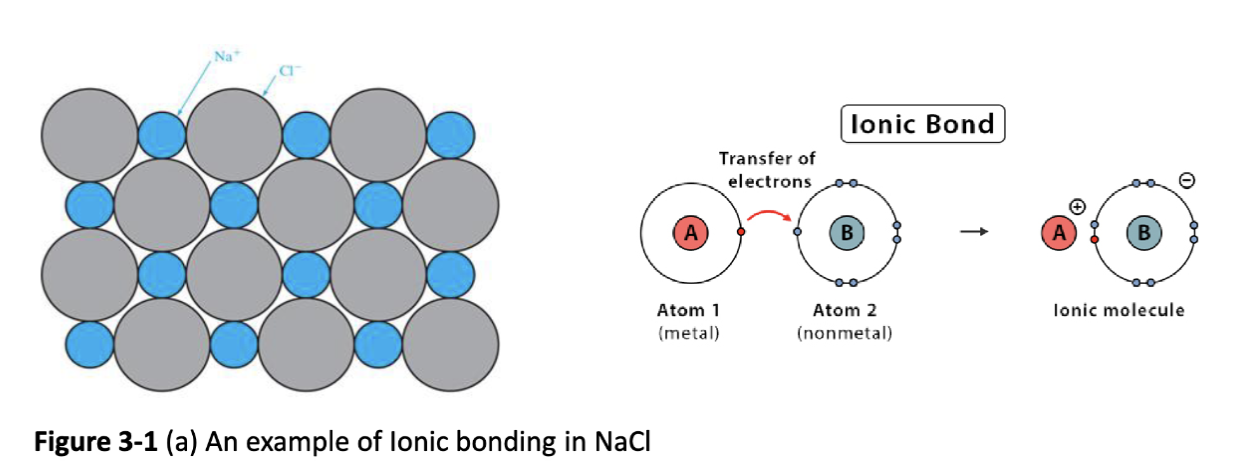
固体中相邻原子之间的电子将晶体结合在一起,比如 NaCl 表现为离子键结合 (ionic bonding)。在离子键中,一个原子向另一个原子提供电子使其保持稳定,电子大部分时间靠近结合的原子。
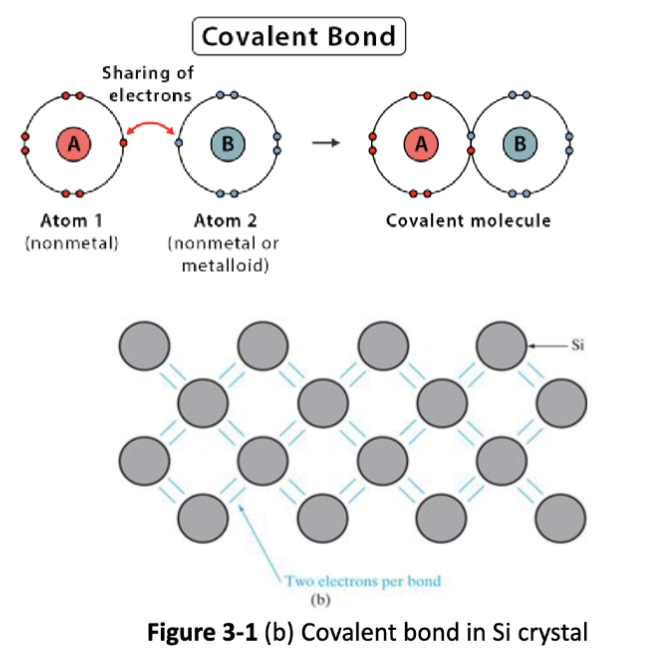
在共价键 (covalent bond) 中,原子通过共享电子来结合。电子在两个原子核之间的空间中移动,形成一个稳定的结合状态。共价键通常比离子键更强,因为电子在两个原子之间共享,使得结合更牢固。比如对于金刚石晶体,每个碳原子通过共价键与四个相邻的碳原子结合,在价电子层形成八个电子的八隅体 (octet) 结构,进而形成一个坚固的三维网络结构。
根据波尔的理论,原子的每一层在不同的能级上有着离散的能量。当两个原子靠的很近时,他们的相互作用会让能级分裂成多个能级,形成一个能带。随着更多原子的加入,能级分裂得越来越细,最终形成连续的能带。在能带中,电子可以在一定范围内自由移动,而不是局限于单个原子。
当原子结合形成物质时,最外层、亚层、轨道会合并,为电子提供更多的可用能级。当大量原子彼此靠近时,这些能级变得如此接近,以至于它们形成了连续的能带。当键能最小时,会形成平衡,这时候两个原子之间的合力为 0,形成稳定的原子间距 (Equilibrium Interatomic Distance)。
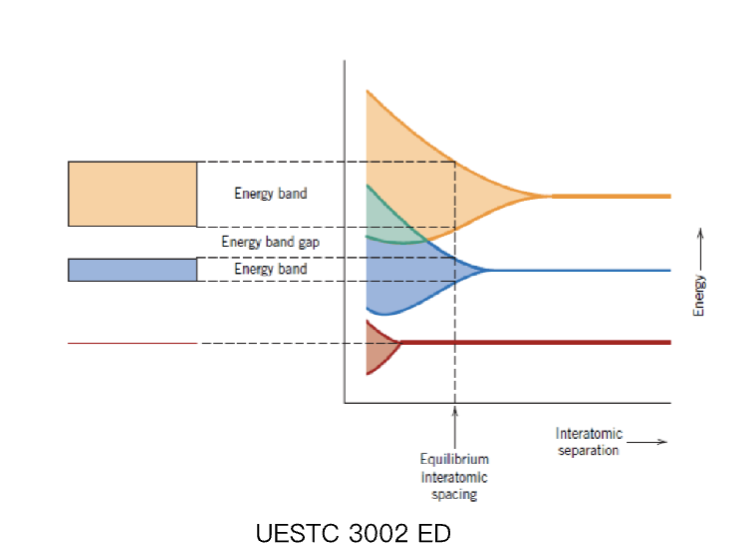
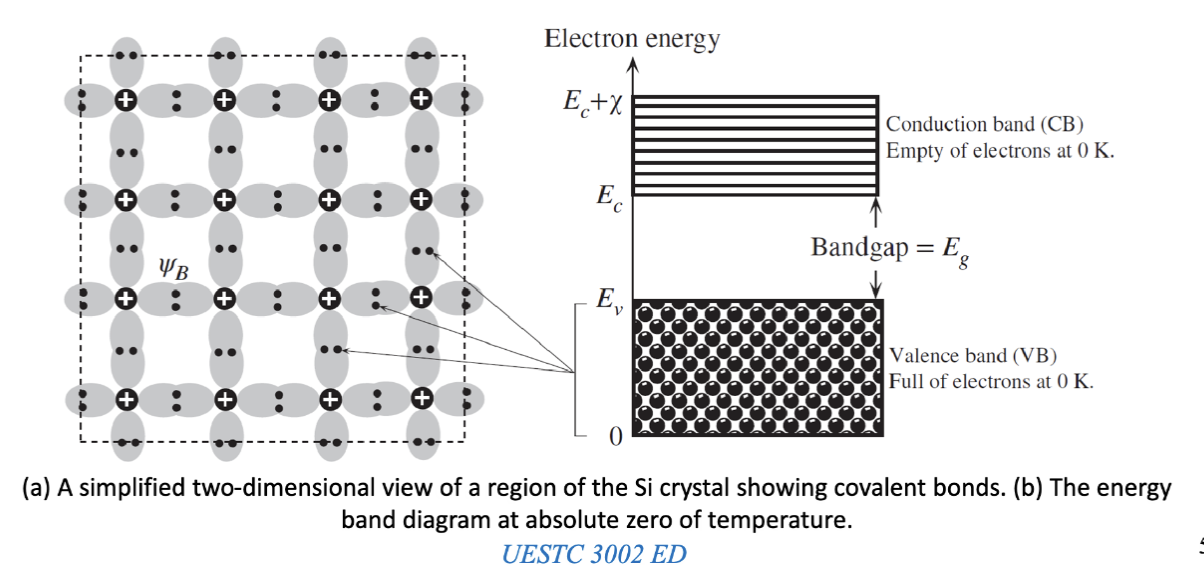
当原子在晶体中紧密排列时,每个能级都会分裂成包含大量紧密排列状态的能带。这些能带被称为禁带 (forbidden gaps) 或带隙 (band gaps) 的禁止能量区域所分隔。完全被电子填满的最后一个能带称为价带 (valence band) 。下一个可能为空或部分被电子填充的能带称为导带 (conduction band) 。
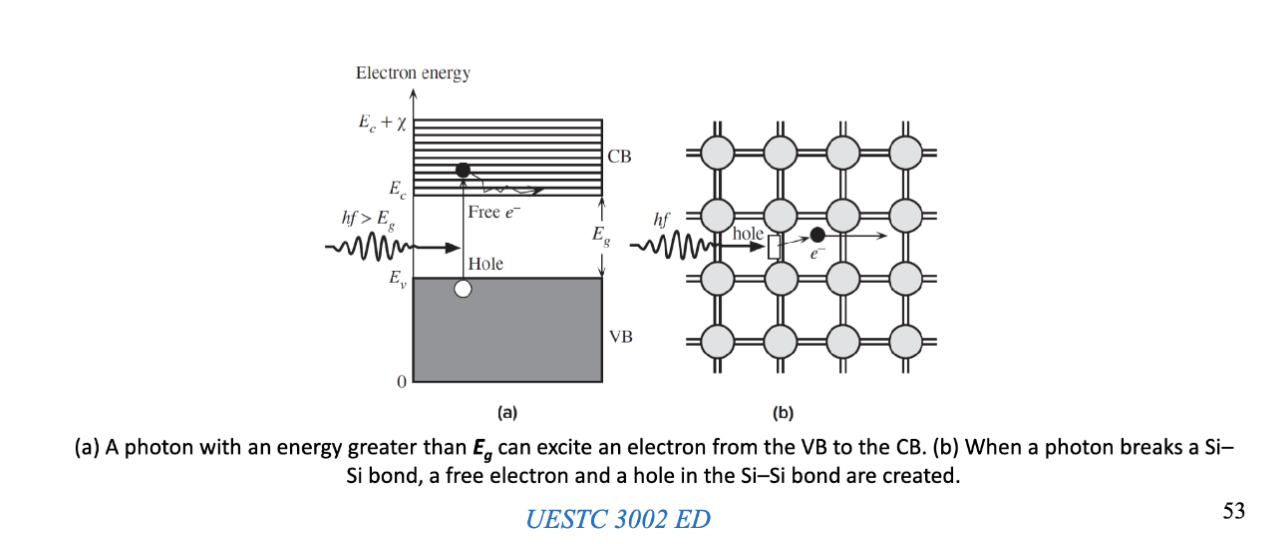
一个原子的最外层电子 (outermost shell) 被称为价电子 (valence electrons),这些价电子包含一系列的能级,形成价带。价带中的电子与原子核的结合较弱,因此它们可以通过吸收能量跃迁到导带。导带中的电子可以自由移动,从而使材料具有导电性。价带好导带之间的间隙被称为禁带 (band gap) 或带隙 (forbidden gap),用 表示。禁带的大小决定了材料的导电性能。禁带没有能量,因此电子不能存在于禁带中。
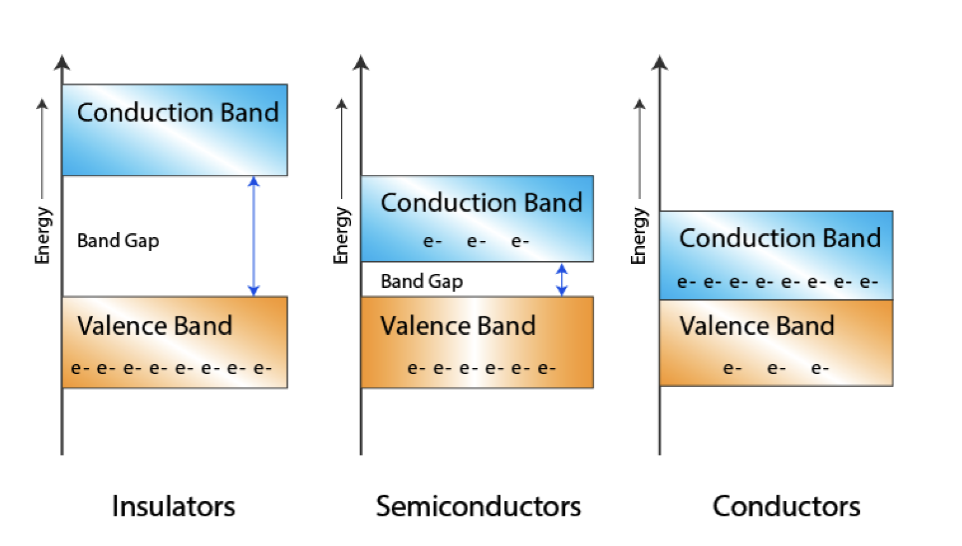
半导体材料在 0K 时性质和绝缘体基本相同,价带被完全填满,导带为空。然而,半导体的 远小于绝缘体,随着温度的升高,一些电子会获得足够的能量跃迁到导带,形成自由电子 (free electrons),这些电子可以在导带中自由移动,从而使材料具有导电性。
半导体的带隙可以是两种类型:直接带隙 (direct band gap) 和间接带隙 (indirect band gap)。在直接带隙半导体中,价带的最高点和导带的最低点在动量空间中位于相同的位置,这使得电子可以直接从价带跃迁到导带,通常伴随着光子的吸收或发射。典型的直接带隙半导体包括砷化镓 (GaAs) 和氮化镓 (GaN)。在间接带隙半导体中,价带的最高点和导带的最低点在动量空间中位于不同的位置,这意味着电子在跃迁过程中需要同时改变其动量,通常通过与晶格振动(声子)的相互作用来实现。典型的间接带隙半导体包括硅 (Si) 和锗 (Ge)。
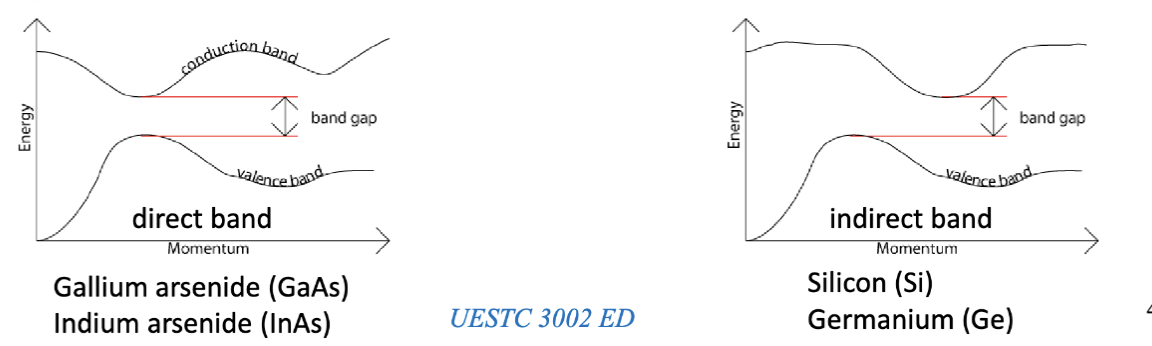
除了 IV 族元素 (如 Si 和 Ge) 之外,III-V 族化合物半导体 (如 GaAs 和 InP) 也非常重要。III-V 族化合物半导体由 III 族元素(如镓 (Ga)、铟 (In))和 V 族元素(如砷 (As)、磷 (P))组成。这些材料通常具有较高的电子迁移率和直接带隙,使其在高速电子器件和光电子器件中具有优势。砷化镓 (GaAs) 是一种重要的 III-V 族化合物半导体,其掺杂可以通过改变 Ga 和 As 的比例来实现,从而调节其电学性质。GaAs 具有较高的电子迁移率和直接带隙,适用于高速电子器件和光电子器件。
和半导体中的载流子
在 0K 时,半导体材料有填满的价带和空的导带。随着温度的升高,一些电子获得足够的能量跃迁到导带,形成自由电子 (free electrons),这些电子可以在导带中自由移动,从而使材料具有导电性。价带中的空位称为空穴 (holes),它们也可以在价带中移动,表现为正电荷载流子。
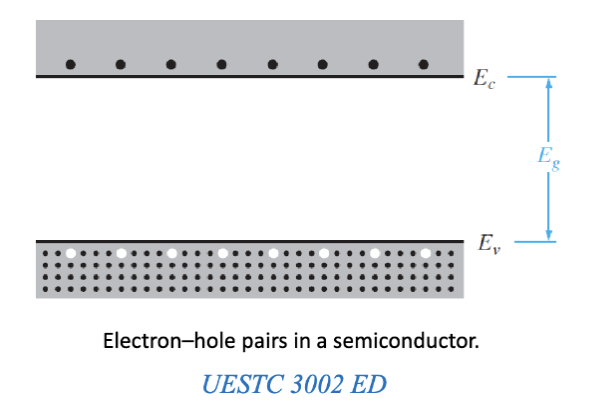
价带和导带之间的能量差称为禁带宽度 (band gap),用 表示,为 。 到真空能级的距离称为电子亲和能 (electron affinity),用 表示。 到真空能级的距离称为功函数 (work function),用 表示。功函数可以表示为 。
空穴和电子是半导体中负责电流传导的载流子 (charge carriers)。电子在导带中移动,而空穴在价带中移动。空穴的运动实际上是价带中电子的缺失,表现为正电荷载流子。空穴收到的原子核的力比电子强,通常有更低的迁移率 (mobility)。
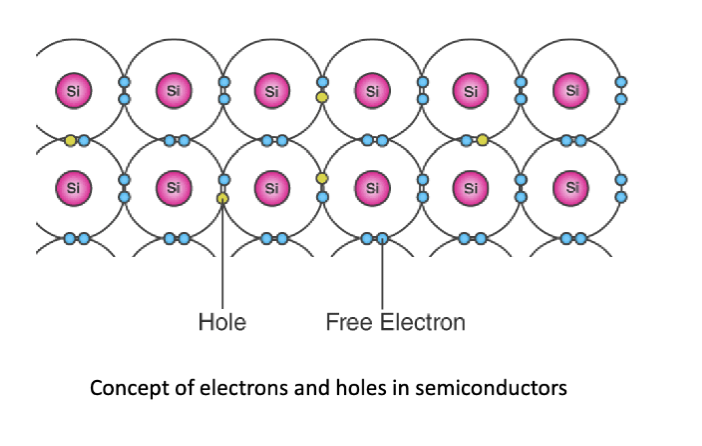
不同种类的半导体
- 可以通过掺杂 (doping) 来调节载流子浓度,从而改变材料的导电性。
- 体积更小,重量更轻,功耗更低。
- 电阻率比金属高,但比绝缘体低。
- 半导体的电阻随着温度升高而降低,表现为负温度系数 (negative temperature coefficient)。
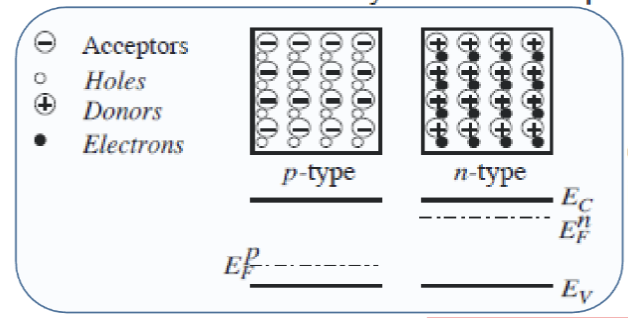
本征半导体 (Intrinsic Semiconductor) 是指纯净的半导体材料,没有掺杂任何杂质。在本征半导体中,载流子浓度主要由热激发产生的电子-空穴对决定。随着温度升高,更多的电子获得足够的能量跃迁到导带,形成自由电子和空穴,从而增加了材料的导电性。比如 Si 和 Ge。他们也称为未掺杂半导体 (undoped semiconductor) 或者 i 型半导体 (i-type semiconductor)。
在纯硅晶体中引入少量杂质称为外延半导体 (Extrinsic Semiconductor)。引入少量的替代原子可以显著提高半导体的导电性。添加杂质原子的过程称为掺杂 (doping)。掺杂可以引入额外的电子或空穴,从而改变材料的导电性。掺杂可以分为两种类型:n 型掺杂 (n-type doping) 和 p 型掺杂 (p-type doping)。
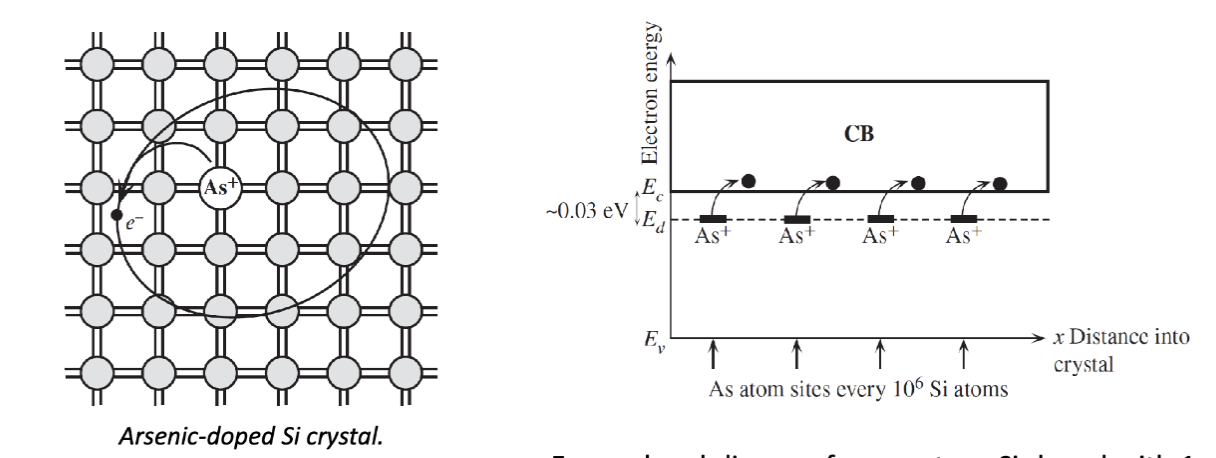
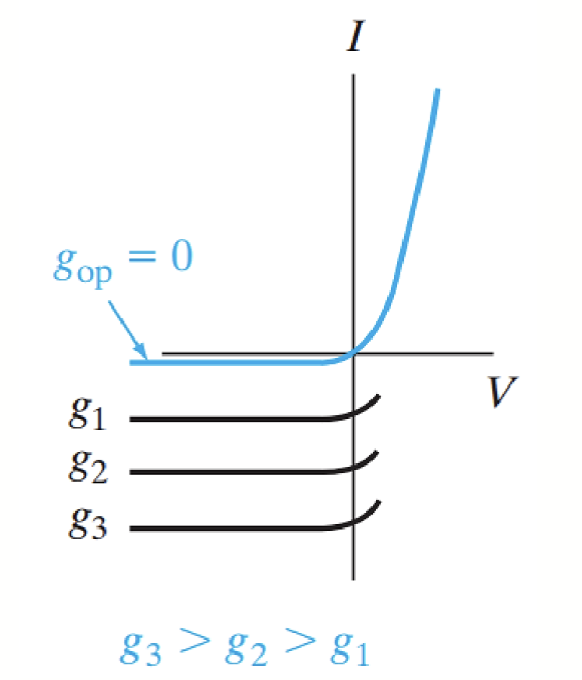
n 型掺杂指的是在半导体中引入五价杂质原子(如磷 (P)、砷 (As)),五价杂质原子有一个额外的价电子,这个电子可以很容易地跃迁到导带,形成自由电子,从而增加了材料的导电性。右图是掺入了 1ppm 的 As 后的能带结构。
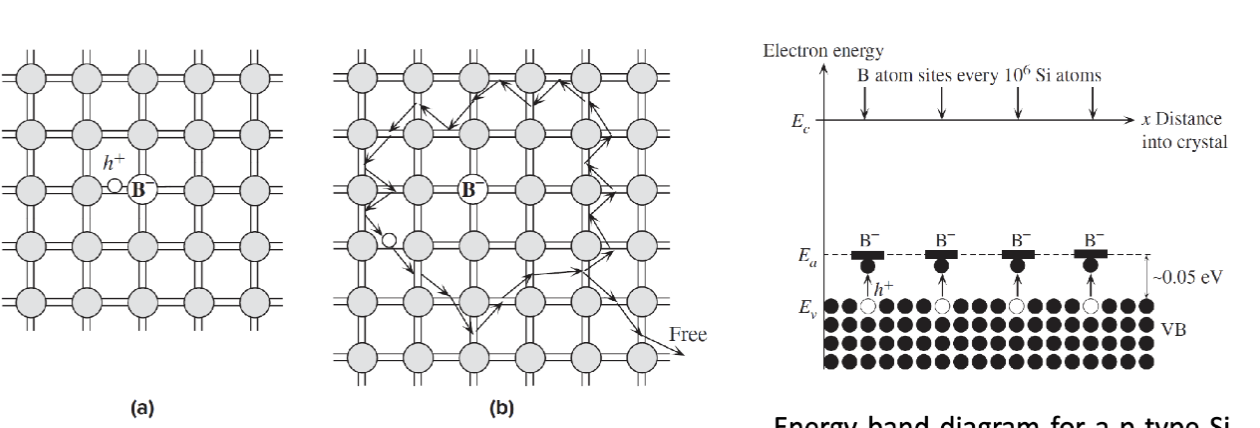
而 p 型掺杂指的是引入三价杂质原子(如硼 (B)、铝 (Al))。三价杂质原子缺少一个价电子,这个缺失形成了空穴,空穴可以在价带中移动,表现为正电荷载流子,从而也增加了材料的导电性。右图是掺杂了 1ppm 的 B 后的能带结构。

泡利不相容原理
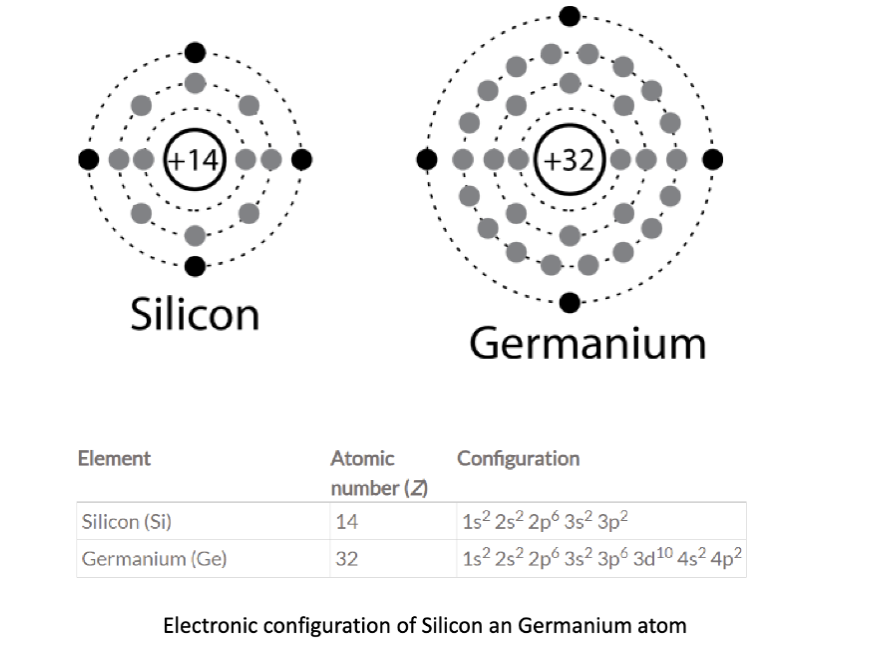
泡利不相容原理指出,在一个原子或分子中,两个或多个费米子 (Fermions) 不能占据完全相同的量子态。费米子是指自旋为半整数(如 1/2, 3/2 等)的粒子,包括电子、质子和中子等。这个原理是量子力学的基本原则之一,由沃尔夫冈·泡利 (Wolfgang Pauli) 在 1925 年提出。具体在这里,指的是单个原子中每个电子都应该有独特的状态:只有两个电子可以占据同一个轨道,但它们必须有相反的自旋 (spin)。
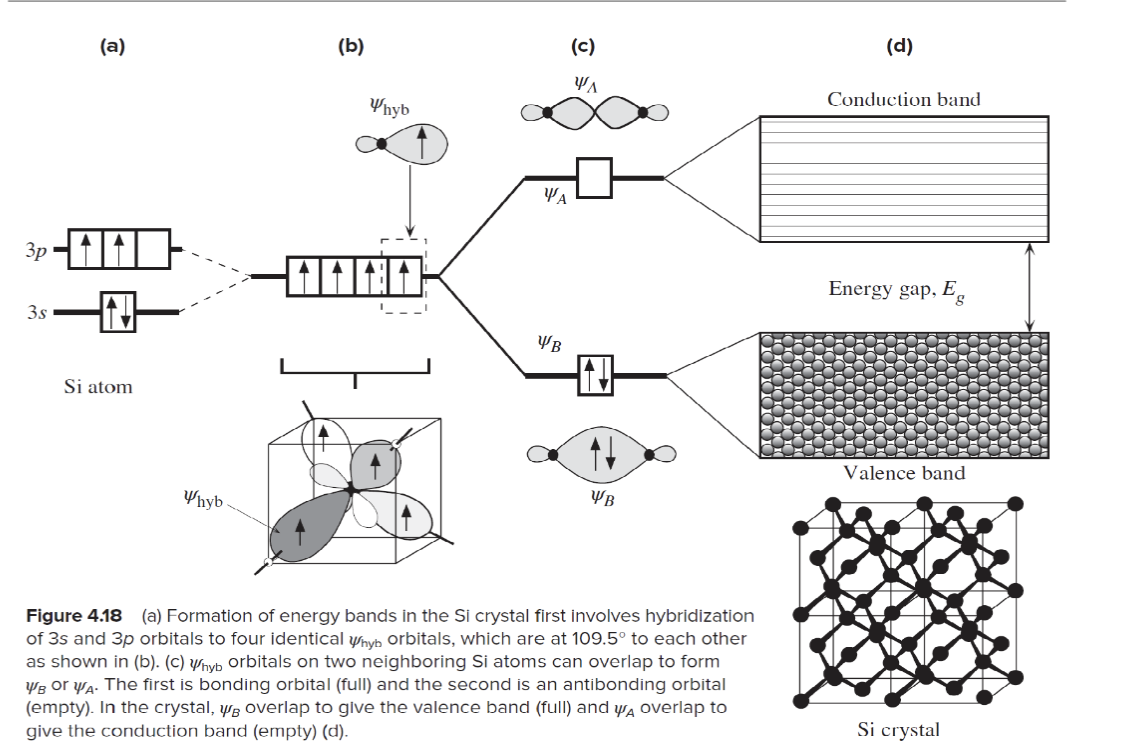
硅原子有 14 个电子,电子排布为 。根据泡利不相容原理,每个轨道最多可以容纳两个电子,且它们必须有相反的自旋。因此,硅原子的电子排布是稳定的。其中, 3s 和 3p 轨道上的电子是价电子 (valence electrons),它们决定了硅的化学性质和导电性能。因为 3s 和 3p 能级非常接近,当硅原子相互接近时,四个价电子会形成四个 杂化轨道,进而形成四个共价键 (covalent bonds),使得硅原子能够与其他硅原子结合,形成坚固的晶体结构。
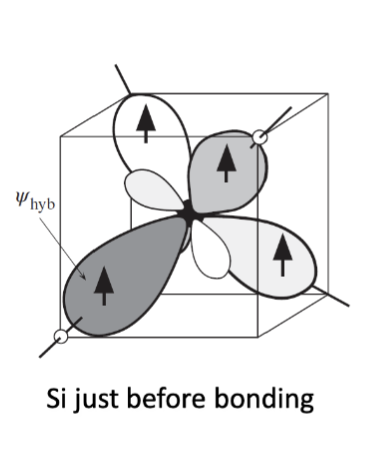
杂化的过程是发生在 和三个 轨道之间的线性组合,形成四个等价的 杂化轨道 。这些杂化轨道有更大的主叶和一个小的后叶,每个杂化轨道都包含一个价电子。四个杂化轨道各有一个价电子,所以是半满结构,这意味着硅原子可以通过共享这些电子与其他硅原子形成共价键,从而形成稳定的晶体结构。
Block 2: Basic Semiconductors
Lec.2.1 P-N Junction Part.1
PN 结的制作过程
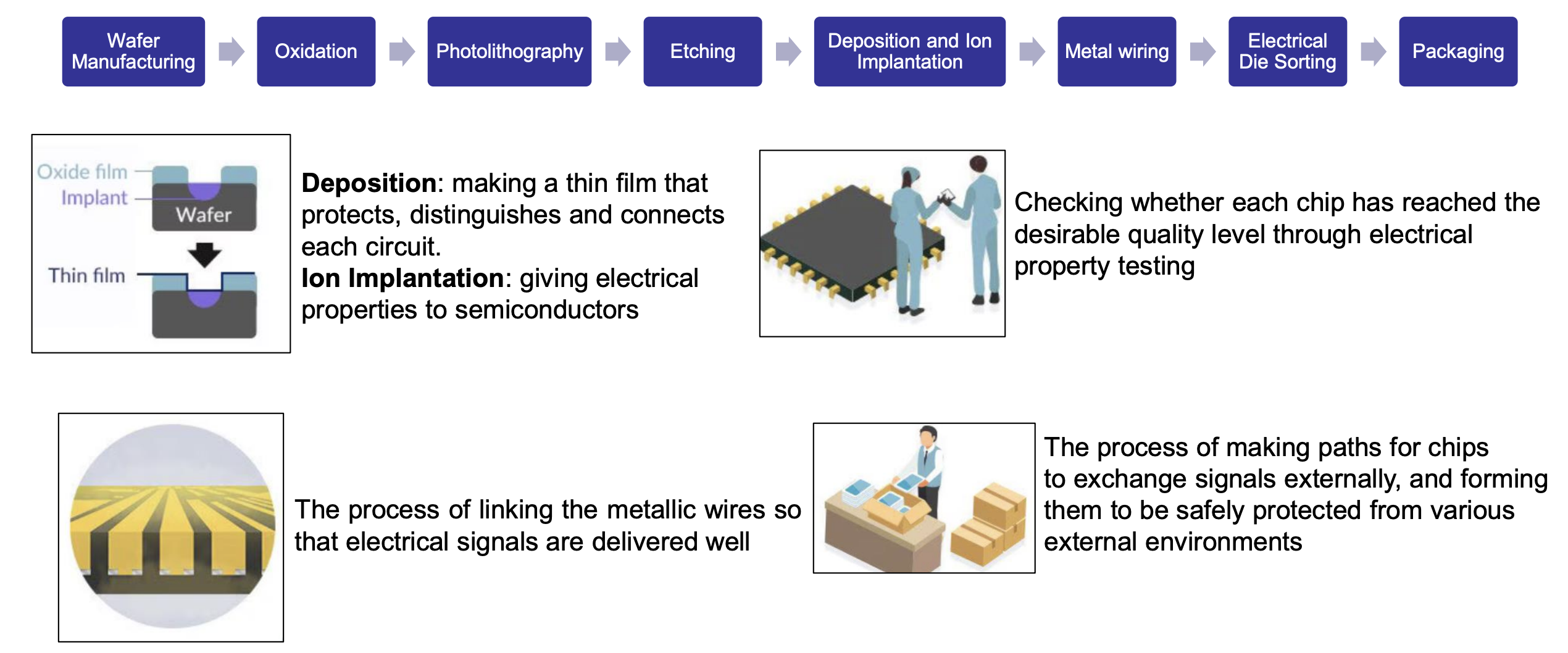
- 晶圆制造 (Water Manufacturing)
- 制造高纯度的单晶硅片 (Wafer)
- 氧化 (Oxidation)
- 在高温下 (1000°C) 将硅片暴露在氧气中,形成一层二氧化硅 (SiO2) 保护层
- 光刻 (Photolithography)
- 在硅片上画出所需图案
- 蚀刻 (Etching)
- 使用化学溶液或等离子体去除不需要的材料
- 沉积 (Deposition) & 离子注入 (Ion Implantation)
- 在硅片上沉积一层薄膜,如多晶硅或金属
- 通过离子注入将掺杂剂引入硅片,形成 P 型和 N 型区域
- 金属互连 (Metal Wiring)
- 在硅片上沉积金属层,形成电极和互连
- EDS (Electrical Die Sorting)
- 测试每个芯片的电性能,确保其符合规格
- 封装 (Packaging)
- 将芯片封装在保护壳中,便于使用和连接
PN 结的介绍
在半导体器件中,P-N 结是由 P 型半导体和 N 型半导体接触形成的界面。P 型半导体富含空穴(正电荷载流子),而 N 型半导体富含电子(负电荷载流子)。当 P 型和 N 型材料接触时,电子从 N 型区域扩散到 P 型区域,与空穴复合,形成一个耗尽区(Depletion Region),该区域内几乎没有自由载流子。
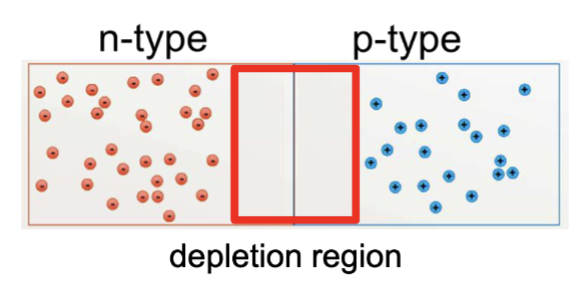
其扩散形成了一个内建电场 (Built-in Electric Field),阻止更多的电子和空穴继续扩散。这个内建电场使得 P-N 结具有整流特性,即允许电流在一个方向上流动,而在相反方向上阻止电流流动。这个电场产生的电势差称为内建电势 (Built-in Potential)。扩散的电荷移动的电流称为扩散电流 (Diffusion Current),而内建电场驱动的电荷移动的电流称为漂移电流 (Drift Current)。在稳态时,扩散电流和漂移电流相等且方向相反,因此净电流为零。
- : 内建电势 (Built-in Potential)
- : 热电压 (Thermal Voltage)
- : 本征载流子浓度 (Intrinsic Carrier Concentration)
- : 玻尔兹曼常数 (Boltzmann Constant)
- : 绝对温度 (Absolute Temperature)
- : 元电荷 (Elementary Charge)
- : 受主浓度 (Acceptor Concentration)
- : 施主浓度 (Donor Concentration)
耗尽层的宽度影响着一个二极管的行为,包括其寄生电容和电场的特性。在稳态时,有:
- : 耗尽层宽度 (Depletion Width)
- : 真空介电常数 (Permittivity of Free Space)
- : 硅的相对介电常数 (Relative Permittivity of Silicon)
- 其他符号同上
在稳态时,半导体是电中性的,也就是说,P 型区域的正电荷总量等于 N 型区域的负电荷总量:
- : P 型区域的耗尽层宽度 (Depletion Width in P-type Region)
- : N 型区域的耗尽层宽度 (Depletion Width in N-type Region)
- 其他符号同上
有,耗尽区基本都在 N 区。因为电荷平衡的倾向,所以电场回让电子从 P 区流向 N 区,空穴从 N 区流向 P 区。
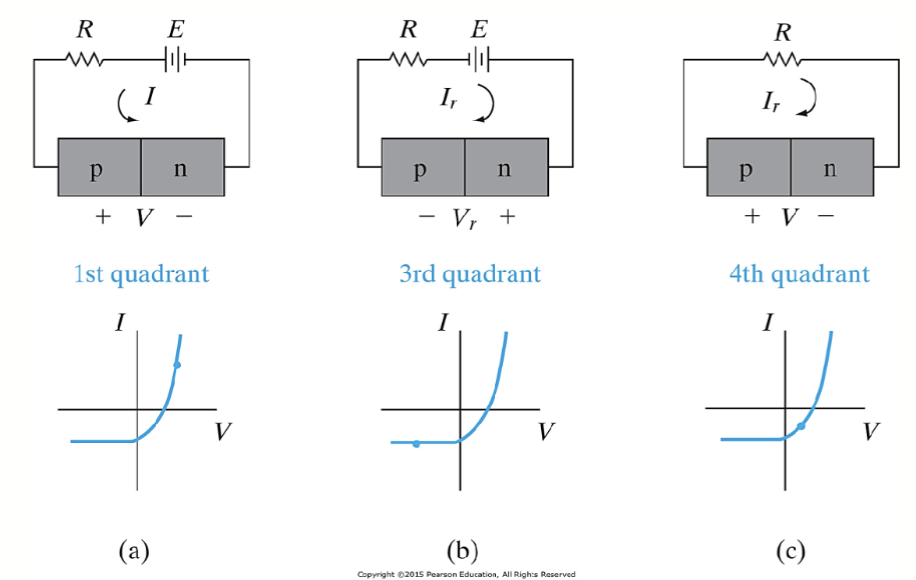
给 PN 结施加外部电压可以控制其内部的电学行为,不同的外部偏置可以改变其耗尽区的宽度。不同的偏执方法有不同的效果:
- 零偏置 (Zero Bias)
- 没有施加外部电压,PN 结处于平衡状态,耗尽区宽度为 。
- 正向偏置 (Forward Bias)
- 施加正电压使 P 型区域连接到电源的正极,N 型区域连接到负极。
- 这会减少耗尽区的宽度,因为外部电压抵消了内建电势,允许更多的载流子通过结。
- 反向偏置 (Reverse Bias)
- 施加负电压使 P 型区域连接到电源的负极,N 型区域连接到正极。
- 这会增加耗尽区的宽度,因为外部电压增强了内建电势,阻止载流子通过结。
在施加电压时,几乎所有的输入电压都会落在耗尽区上,因此耗尽区的宽度可以通过以下公式计算:
- : 施加的外部电压 (Applied External Voltage)
- 其他符号同上
耗尽层宽度越小,耗尽层的电势差越小,载流子更容易跨越 PN 结,从而增加电流流动,扩散电流大小也就越大。反之,耗尽层宽度越大,电势差越大,载流子更难跨越 PN 结,减少电流流动。
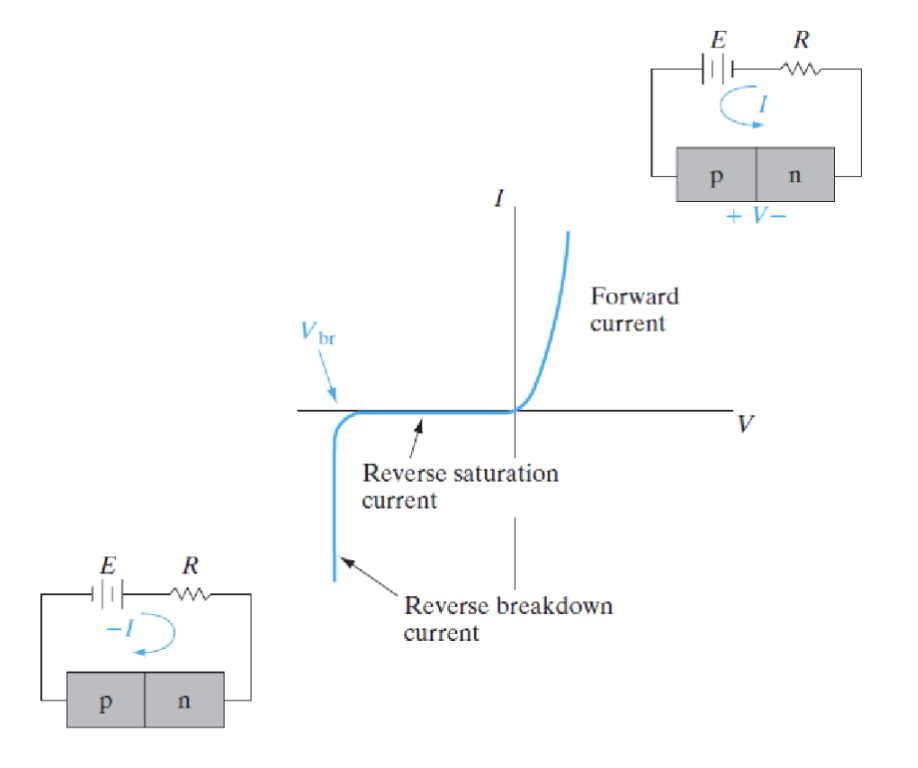
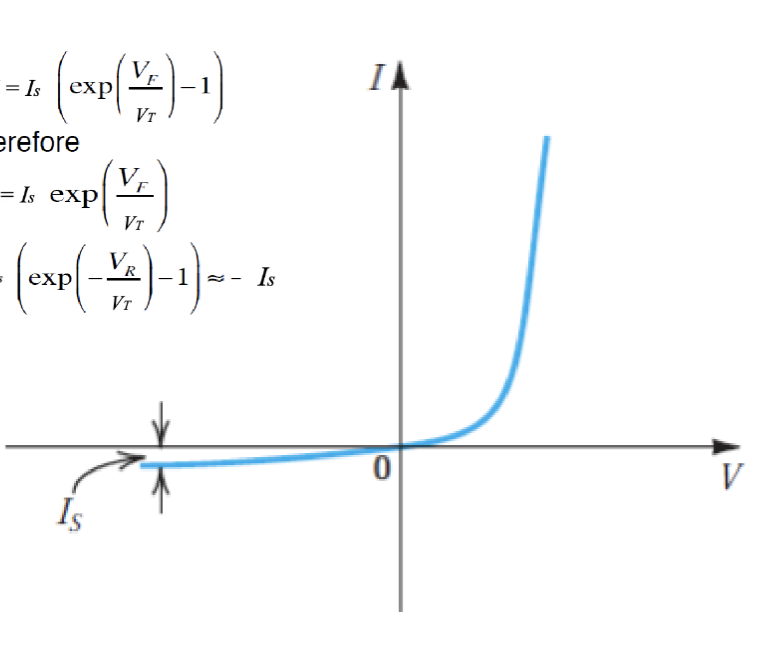
对于一个理想的二极管,其电流-电压关系可以用肖克利方程 (Shockley Equation) 描述:
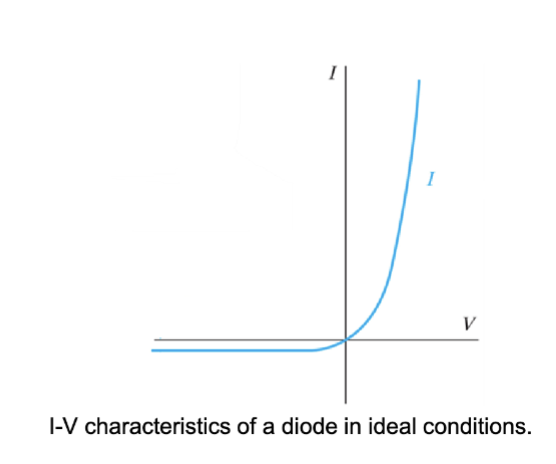
- : 二极管电流 (Diode Current)
- : 反向饱和电流 (Reverse Saturation Current)
- : 施加的外部电压 (Applied External Voltage)
- 其他符号同上
在正向偏置下,电流随着电压的增加呈指数增长,而在反向偏置下,电流接近于 ,表示非常小的反向漏电流。
Lec.2.2 P-N Junction Part.2
PN 结的结电容
回顾一下 Lec.2.1 中提到的 PN 结相关的几个公式:
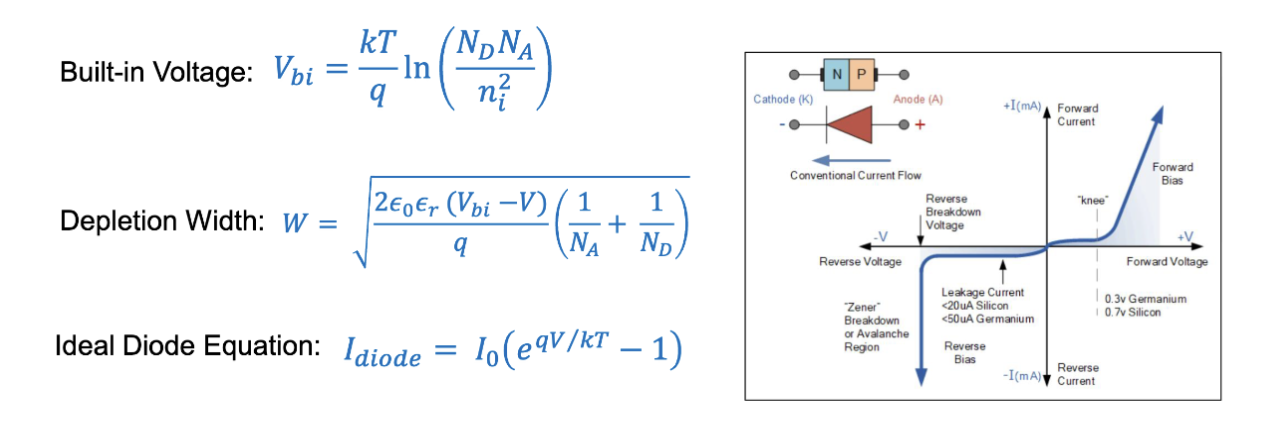
在耗尽层的两侧,电荷相互间隔,形成了一个电容器,其电容值可以通过以下公式计算:
- : PN 结的结电容 (Junction Capacitance)
- : 半导体的介电常数 (Permittivity of the Semiconductor)
- : PN 结的面积 (Area of the PN Junction)
- 其他符号同上
在 PN 结中有 ,所以可以简化为:
因此,测量二极管中的电容大小是一种间接测量掺杂浓度 的方法。
载流子在电场作用下的运动
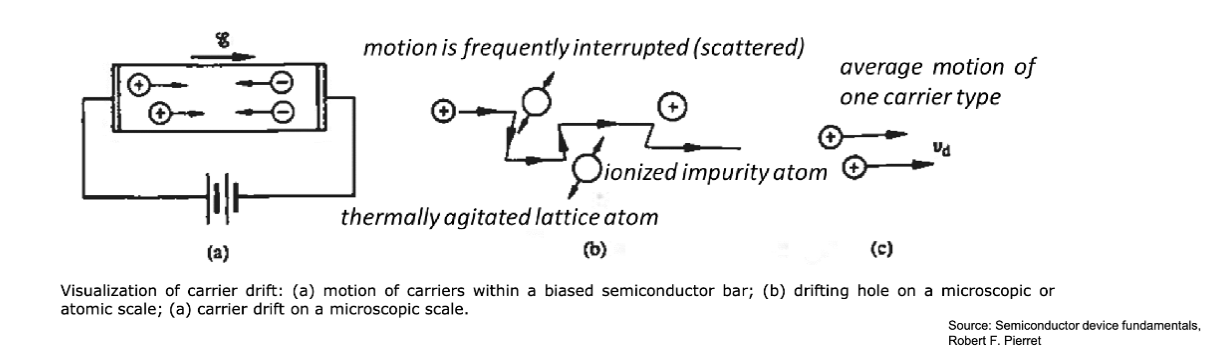
在半导体内部,载流子的行为主要分为两种
- 漂移 (Drift)
- 载流子在电场作用下的运动
- 例如,在 PN 结的耗尽区内,电场会使电子向 N 区移动,空穴向 P 区移动
- 扩散 (Diffusion)
- 载流子由于浓度梯度而发生的运动
- 例如,在 PN 结的两侧,载流子会从高浓度区域扩散到低浓度区域
漂移
在施加了外部电场 的情况下,电场力会对载流子施加作用力。这个力叠加在电子的随机作用上,可以看作粒子以一个恒定的平均漂移速度运动
施加在粒子上的力的大小为 ,引起的加速度大小是 。电场的加速作用同时由粒子的质量和电荷决定,也就是质荷比。在半导体中,质量用 表示,称为 有效质量 (Effective Mass)。其由半导体的能带结构决定。
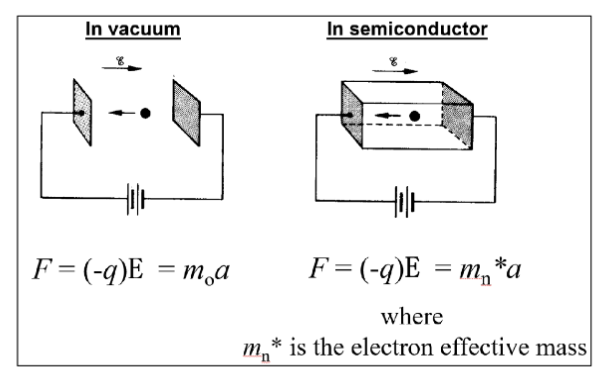
漂移速度 (Drift Velocity) 指的是当施加电场时材料中载流子的速度。在低电场下有公式:
其中, 是载流子的迁移率 (Mobility),表示载流子在电场作用下的响应能力。迁移率的单位是 。在半导体材料中,电子和空穴的迁移率 和 通常不同,通常取决于温度、掺杂浓度和其他因素等。
漂移电流密度 (Drift Current Density) 指的是由于电场的影响,半导体中的载流子的运动引起的单位面积的电流的流动。对于电子和空穴,漂移电流密度可以表示为:
总的漂移电流密度为:
扩散
扩散 (Diffusion) 指的是载流子的热运动引起的,从高浓度区域向低浓度区域的净移动过程。这种现象是由于载流子在材料中的随机热运动所导致的。在半导体中,扩散电流密度 (Diffusion Current Density, ) 可以用菲克定律 (Fick’s Law) 来描述:
从公式可以看出,扩散电流大小取决于浓度梯度大小和相应的载流子的扩散系数。其中, 和 分别表示电子和空穴浓度关于位置 的变化率, 和 分别是电子和空穴的扩散系数,单位是 。
扩散系数 (Diffusion Coefficient, 和 ) 描述了载流子在浓度梯度作用下在材料中扩散的难易程度。其与迁移率之间存在爱因斯坦关系 (Einstein Relation):
两者都取决于载流子迁移率 和 以及温度 。更高的迁移率会导致更高的扩散率。这种关系将载流子的热运动(也就是扩散)和其对电场的响应(也就是迁移)联系起来。
总载流子电流
半导体中的总载流子电流密度 (Total Carrier Current Density) 是漂移电流密度和扩散电流密度的总和。对于电子和空穴,净载流子电流密度可以表示为:
电导率和电阻率
电导率 (Conductivity, ) 指的是电流密度 与施加在材料上的电场大小 之间的比例系数。半导体的总电导率的计算方式是:
其中, 和 分别是材料中电子和空穴的浓度, 和 分别是电子和空穴的迁移率。
对应的,电阻率 (Resistivity, ) 是电导率的倒数,它衡量得失材料对电流流动的阻碍程度。它受载流子数量以及其在材料中的移动难易程度,也就是迁移率的影响。电阻率的计算方式是:
但是,怎么确定电子浓度和空穴浓度?
过程涉及到态密度 (Density of States, ) 和状态占据概率 (Occupation Probability, )。最终的计算方式是将二者相乘并积分:
在此处, 是导带的底部能级, 是一个足够大的能量范围,确保包含了所有可能的电子态。通过这个积分,我们可以计算出在给定条件下材料中的电子浓度 。
此处费米函数 (Fermi Function) 描述了占据可用能级的概率:
其中, 是费米能级 (Fermi Level),表示在绝对零度下电子填充到的最高能级。 是玻尔兹曼常数, 是绝对温度。
而态密度的定义是可用能级的数量,进而决定有多少电子可以到达导带。其计算方式为:
其中, 是电子的有效质量, 是普朗克常数, 是导带的底部能级。
把这些定义带入上述的积分公式中,可以计算出材料中的电子浓度 。类似地,可以通过类似的积分计算出空穴浓度 。
这里有
这里电子的有效质量 值是 。 被称为导带有效态密度 (Effective Density of States in the Conduction Band),表示在导带中可用的电子态的数量。
可以对价带中的空穴密度进行类似的计算。将价带中的态密度 和费米函数 与 1 的差相乘并积分,得到空穴浓度 :
因为电子缺失的概率是 ,同时也是单位能量中的空穴浓度。而电子出现的概率是 ,所以 就是空穴出现的概率。
假定 比 高几个 ,可以得到近似解:
这里有
被称为价带有效态密度 (Effective Density of States in the Valence Band),表示在价带中可用的空穴态的数量。 是空穴的有效质量。
使用空穴密度和电子密度的表达式,计算出本征载流子浓度 (Intrinsic Carrier Concentration):
本征半导体是一种纯净的半导体晶体,电子和空穴对浓度相同,几乎不含杂质,费米能级位于禁带中间。此处的 就是本征载流子浓度。
已严肃被绕晕
课上练习:
Lec.2.3 P-N Junction Part.3
PN 结的能带图
由于扩散效应,能带会在 PN 结处弯曲,形成势垒。导带和价带的 n 型区域(N 区)相对于 p 型区域(P 区)更低。如果电流想要流动,电子必须克服这个势垒。
在两侧的费米能级必须相等。这是热力学平衡的要求。
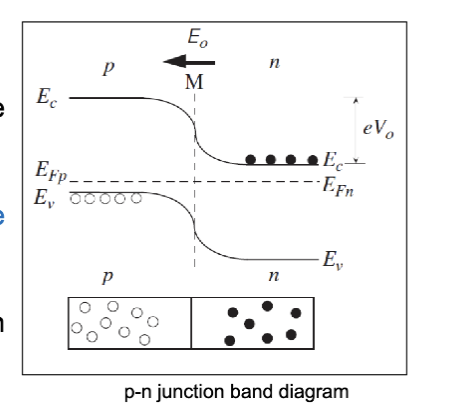
在正向偏置时,施加的电压和内建电势相反,让势垒降低,更多的载流子能够进入结中,耗尽区变窄,电流增大。两侧费米能级不对齐,n 区的费米能级高于 p 区的费米能级。两者的差值大小等于外加电压做功 。
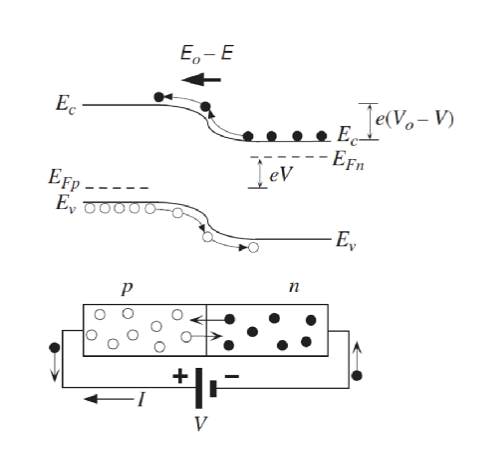
在反向偏置时,施加的电压和内建电势同向,让势垒增大,载流子更难进入结中,耗尽区变宽,电流减小。在这种情况下,只有少数载流子会对微小的反向饱和电流做出贡献。故电流大小几乎不受反向偏置电压的影响。
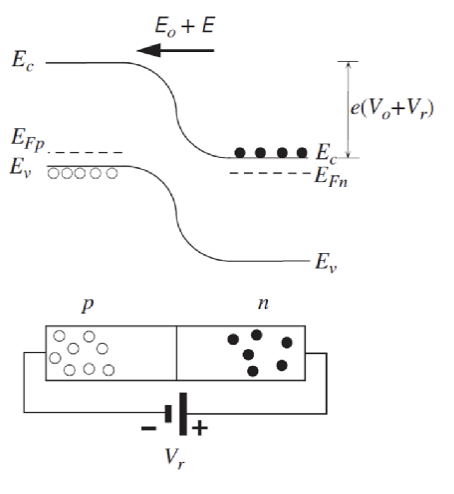
热生成 (Thermal Generation) 是指在热激发下,价带中的电子获得足够的能量跃迁到导带,形成电子-空穴对的过程。这个过程在 PN 结中尤为重要,因为它是反向饱和电流的主要来源。
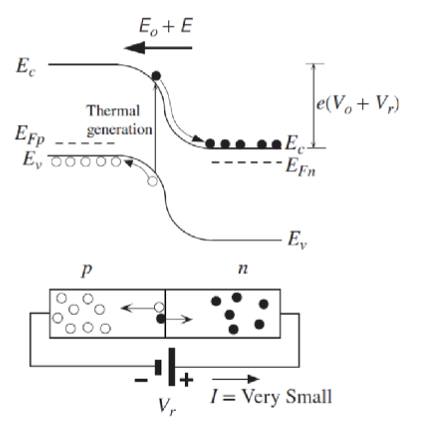
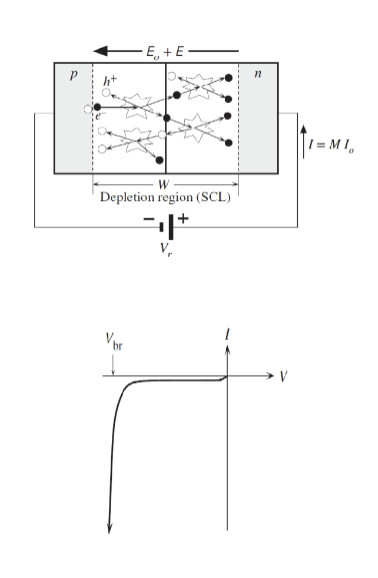
反向击穿 (Reverse Breakdown) 是指在反向偏置下,PN 结中的电场强度增大到一定程度,导致载流子获得足够的能量,产生雪崩效应或隧穿效应,从而引发大量载流子流动,导致电流急剧增加的现象。
在耗尽区的电场变得非常大,以至于这个区域内的漂移电流中的电子获得足够的动能,能够碰撞电离晶格中的原子,产生更多的电子-空穴对。这种连锁反应导致电流迅速增加,称为雪崩击穿 (Avalanche Breakdown)。
齐纳击穿指的是在重掺杂的 PN 结中,由于能带弯曲剧烈,导致价带和导带在耗尽区内非常接近,甚至重叠。这样,电子可以通过量子隧穿效应直接从价带跃迁到导带,形成大量载流子流动,导致电流急剧增加的现象。这种情况下产生电流的现象叫做齐纳效应 (Zener Effect)。齐纳效应对于齐纳二极管的运行至关重要,因为它允许二极管在特定的反向电压下稳定工作,起到稳压的作用。
练习题

一个硅晶体的 PN 结的施主浓度和受主浓度分别为 ,。求:
- 300 K 区域内的 p 和 n 区域内的费米能级
- 画一个等效的能带图,从图中确定接触电势
- 比较 b 中得到的 和理论计算值
解答:
-
计算费米能级
计算的原理是,费米能级与本征能级的差值可以通过载流子浓度与本征载流子浓度的比值来计算。这个公式是耗尽电容那个公式变形来的。
-
能带图
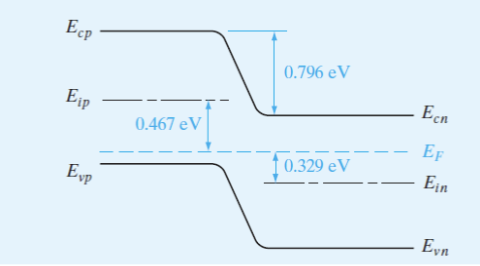
其中,接触电势是两侧费米能级的差值:
-
理论计算值
以防忘记费米能级怎么算。
Lec.2.4 P-N Junction Part.4
复合 (Recombination)
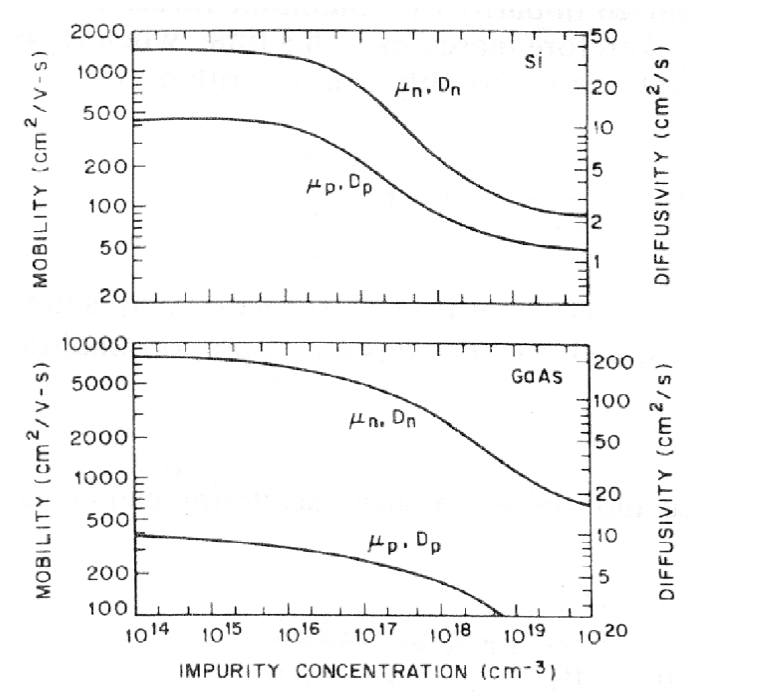
这两张图展示了电子和空穴在两种半导体材料 (Si 和 GaAs) 中的移动性随着掺杂浓度的变化情况。在 GaAs 中,有效质量更小,进而在相同的杂质浓度下有了更高的 和 。
在之前提到了半导体中的总电流是电子和空穴电流的总和:
在发生扩散的过程中,电子会发生复合 (Recombination),也就是电子和空穴相遇的时候。电子和空穴结合会生成中性的原子,从而减少了自由载流子 (Free Carrier) 的数量。
通常会使用一个特征的时间 来表示复合效应,成为电子复合寿命 (Electron Recombination Lifetime)。之后可以给根据电子和空穴的寿命来定义扩散长度 (Diffusion Length):
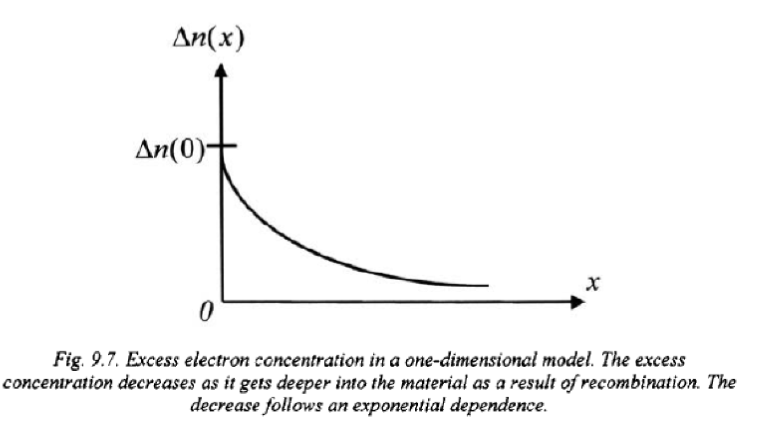
这里的 和 分别表示空穴和电子的扩散长度。扩散长度表示载流子在复合之前可以移动的平均距离。
耗尽电容 (Depletion Capacitance)
如果一开始让 PN 结的两部分分开,两部分都是电中性的。p 区里已电离的受主(负电荷)被空穴(正电荷)抵消,n 区里已电离的施主(正电荷)被电子(负电荷)抵消。这个时候
这个时候,两侧的费米能级的距离是
其中, 和 分别是 n 区和 p 区的费米能级, 和 分别是施主和受主的掺杂浓度, 是本征载流子浓度。
在两侧接触后,电子会从 n 区扩散到 p 区,空穴会从 p 区扩散到 n 区。由于载流子的扩散,导致两侧靠近接触面的区域出现了电荷不平衡的现象。在 n 区靠近接触面的区域,有多余的正电荷(已电离的施主),而在 p 区靠近接触面的区域,有多余的负电荷(已电离的受主)。这些多余的电荷形成了空间电荷区 (Space Charge Region),也称为耗尽区 (Depletion Region)。
在平衡状态下,漂移电流和扩散电流相互抵消,PN 结內产生了一个内建电势 (Built-in Potential) 。支持这个结电场的势垒高度被称为接触电势 (Contact Potential)。
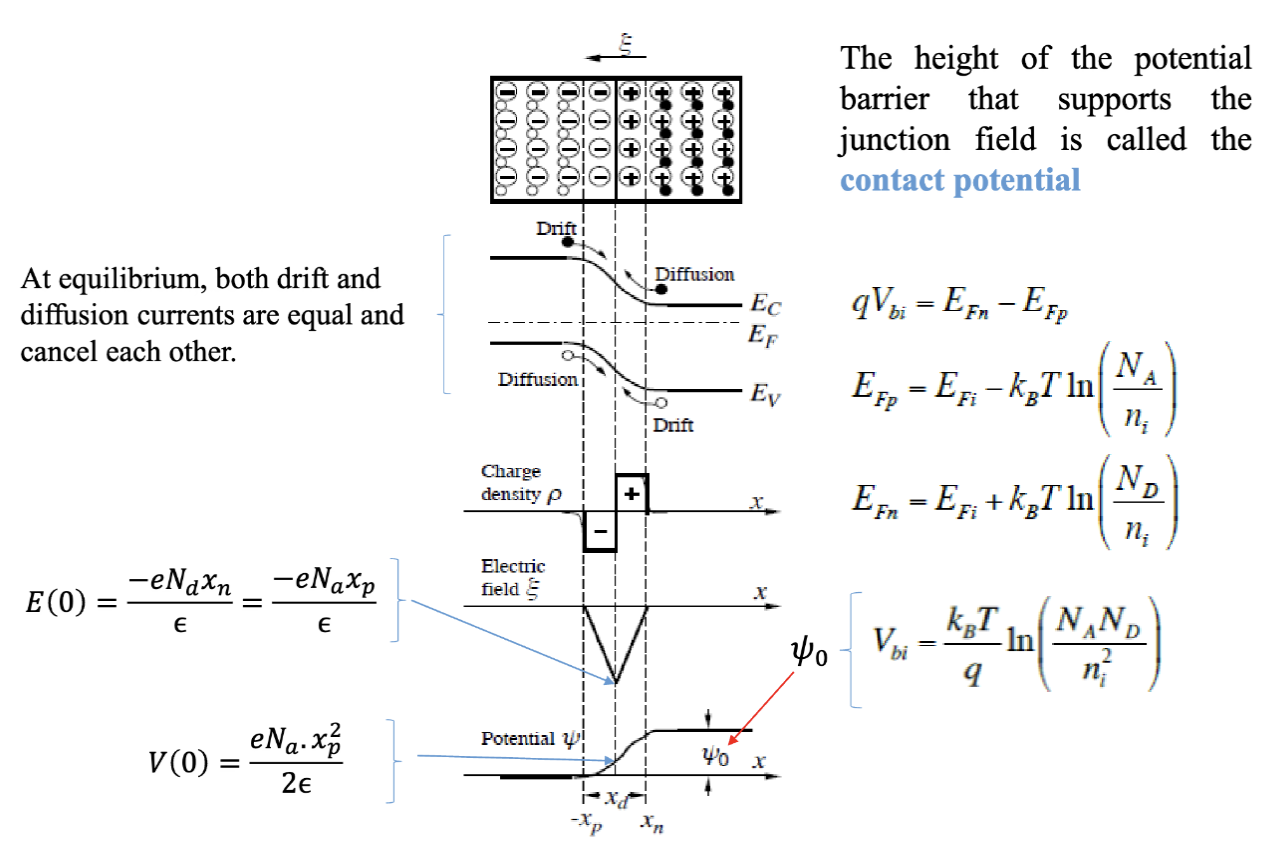
由于达到了平衡状态,耗尽区内没有移动载流子。在耗尽近似 (Depletion Approximation) 下,区域内的电荷密度等于已电离的受主或者施主的电荷密度。
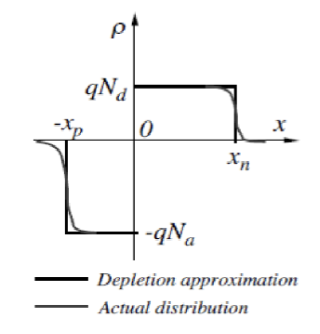
为了求出 和 ,也就是耗尽区在 p 区和 n 区的宽度,可以使用泊松方程 (Poisson’s Equation):
其中, 是真空介电常数, 是半导体的相对介电常数, 是基本电荷量, 是外加电压, 是内建电势,也就是 。
所以,耗尽区的总宽度是
因此,空间电荷层中的小信号电容,可以用这个公式来表示:
这里, 是耗尽区内的单极电荷总量
化简,可以得到,二极管的耗尽电容大小为
伏安特性 (I-V Characteristics)
在平衡状态下,电子电流的漂移和扩散分量方向相反,大小相同,净电流大小为零。对于空穴也如此。
在外部施加正向偏置时,耗尽区减小,电场减小,进而漂移电流减小。有外部电子注入到 p 区,空穴注入到 n 区。净电流不为零,形成正向电流。
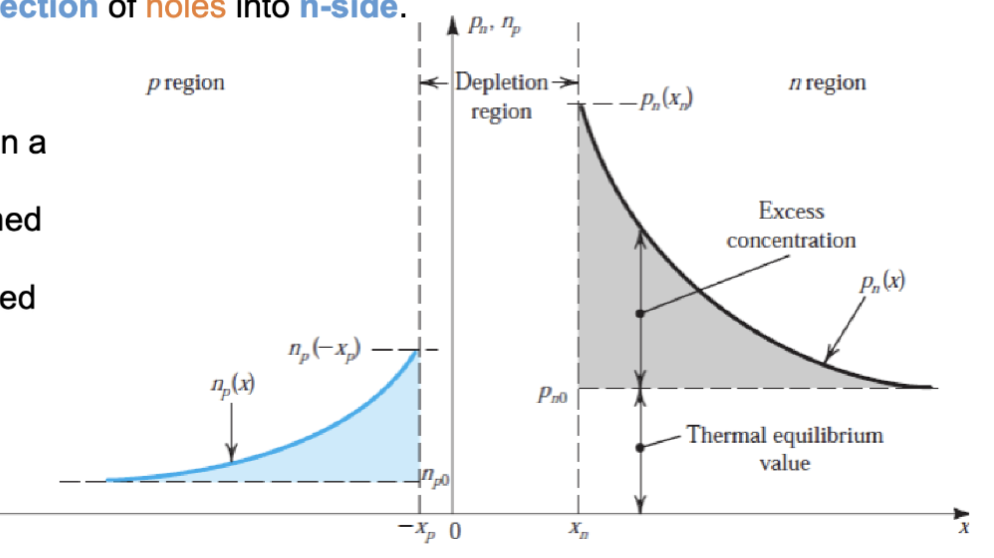
由于电流的特性,通过一个元件的电流应该是处处相等的。所以在 PN 结的任意位置,电子电流和空穴电流的总和应该是相等的:
这个关系叫做肖克利关系 (Shockley Relationship)。这意味着,在远离耗尽区边缘的区域,少数载流子的扩散电流会逐渐通过复合过程变成多数载流子的漂移电流。
当空穴扩散到 n 区时,有:
同样得到电子在 p 区的扩散电流为:
这种情况下,总电流大小为
提取出一个饱和电流 (Saturation Current) ,可以得到 PN 结的 I-V 特性方程:
最终得到了著名的肖克利方程 (Shockley Equation)。这里的 同时也是反向偏置时的电流大小。
总计一下上文提到的一堆公式,最终得到的是这样的结果:
在 n 区,空穴浓度分布为:
在 p 区,电子浓度分布为:
其中 是少数载流子的扩散长度。少数载流子的扩散电流为:
在耗尽层边缘处且处于低注入水平时,有:
且 。
因此,耗尽层边缘的少数载流子电流为:
最终,PN 结的总电流为:
通常,在 时,可以近似为:
在反向偏置时,有
Block 3: Semiconductor Devices
双极晶体管
晶体管的分类
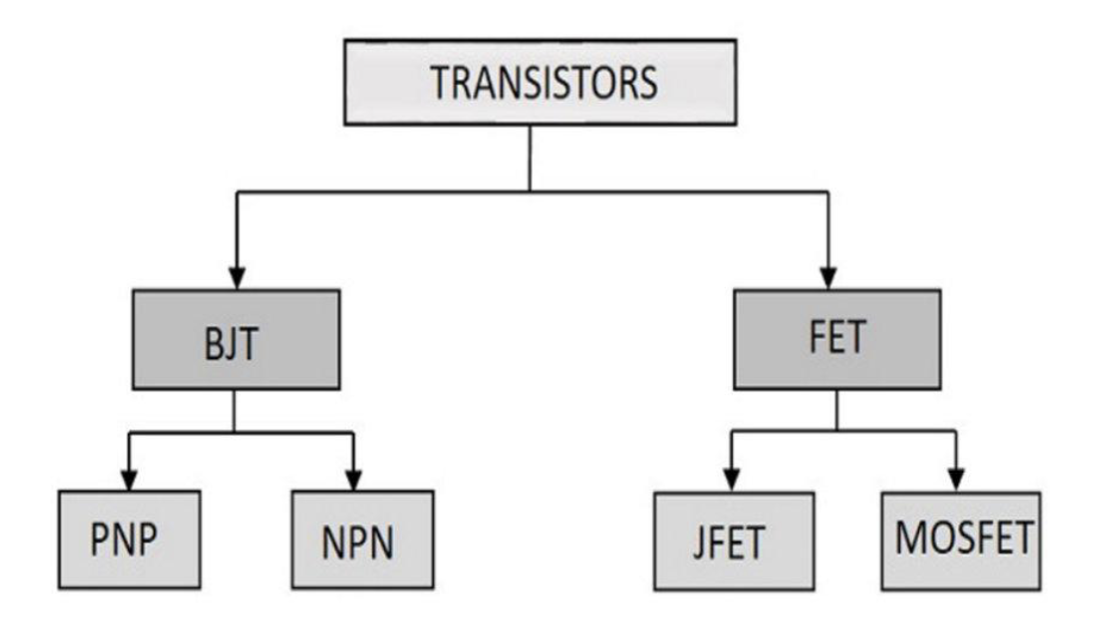
晶体管可以分成两个大类: BJT (Bipolar Junction Transistor) 和 FET (Field Effect Transistor),即双极结型晶体管和场效应晶体管。BJT 可以分为 PNP 和 NPN 两种类型,而 FET 则可以分为 JFET (结型场效应晶体管) 和 MOSFET (金属氧化物半导体场效应晶体管)。
双极晶体管概述
BJT 最早在 1948 年于贝尔实验室发明,被用于多种电子设备。其主要被用于放大和开关电路中。
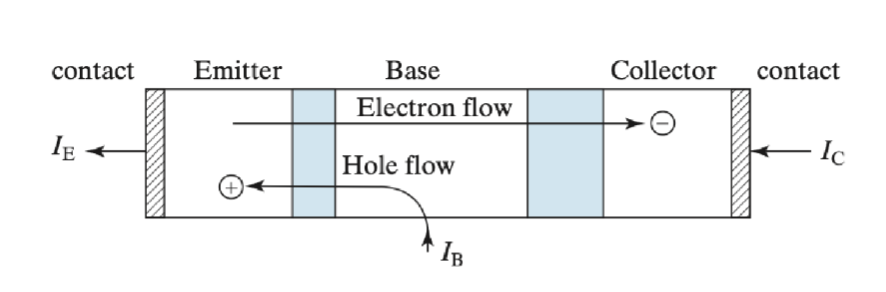
BJT 的结构可以看作是两个二极管的组合,两个二极管共享了一个公共区域,称为基极 (Base)。另外两个区域分别称为发射极 (Emitter) 和集电极 (Collector)。共享的区域可以是二极管的 N 区或 P 区,形成 NPN 或 PNP 结构,分别构成 NPN 型和 PNP 型晶体管。
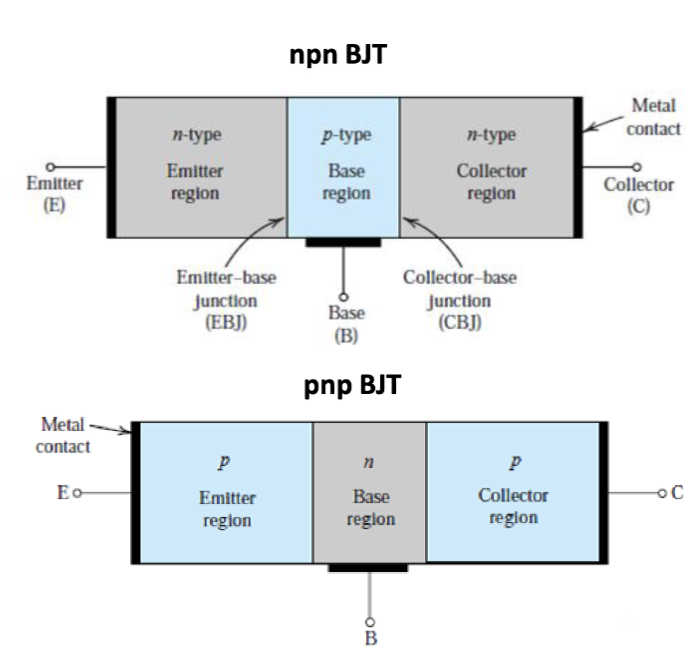
其电路图符号以及典型的工作场景如下:
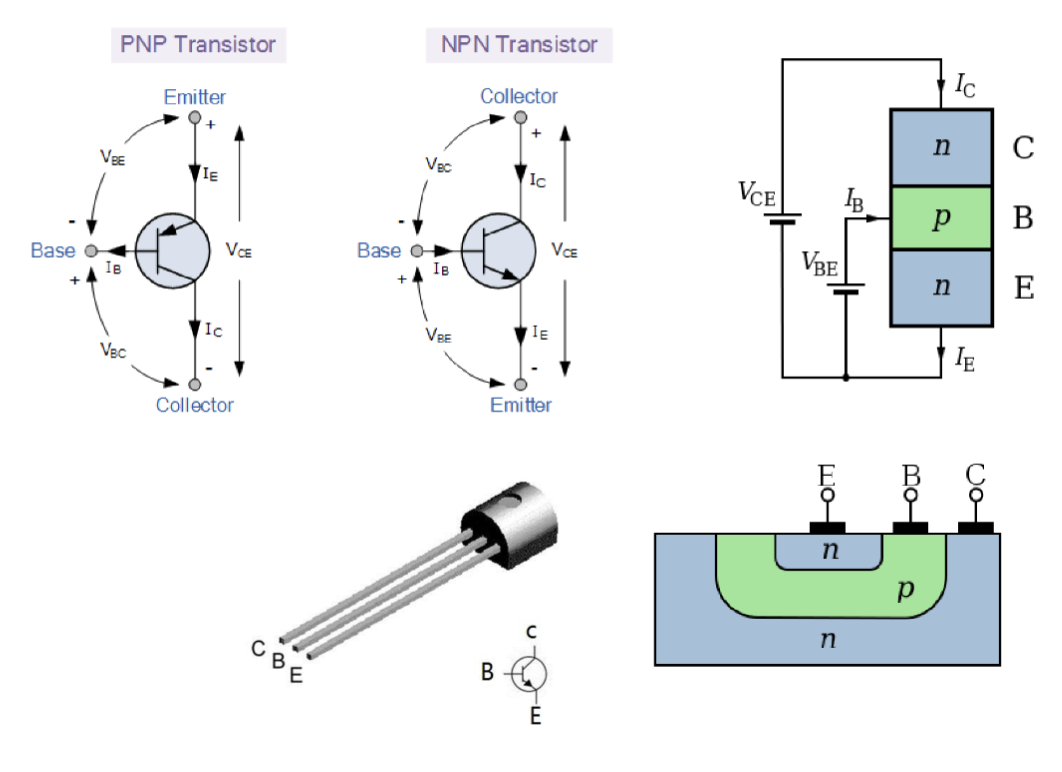
BJT 一共有四种工作模式,分别是饱和 (Saturation)、正向放大 (Forward Active)、截止 (Cut-off) 和反向(Reverse) 模式。不同的工作模式对应不同的偏置条件:
| 工作模式 | 发射结偏置 | 集电结偏置 |
|---|---|---|
| 饱和 (Saturation) | 正向 | 正向 |
| 正向放大 (Forward Active) | 正向 | 反向 |
| 截止 (Cut-off) | 反向 | 反向 |
| 反向 (Reverse) | 反向 | 正向 |
通常,BJT 会工作在正向放大模式下,此时发射结为正向偏置,集电结为反向偏置。
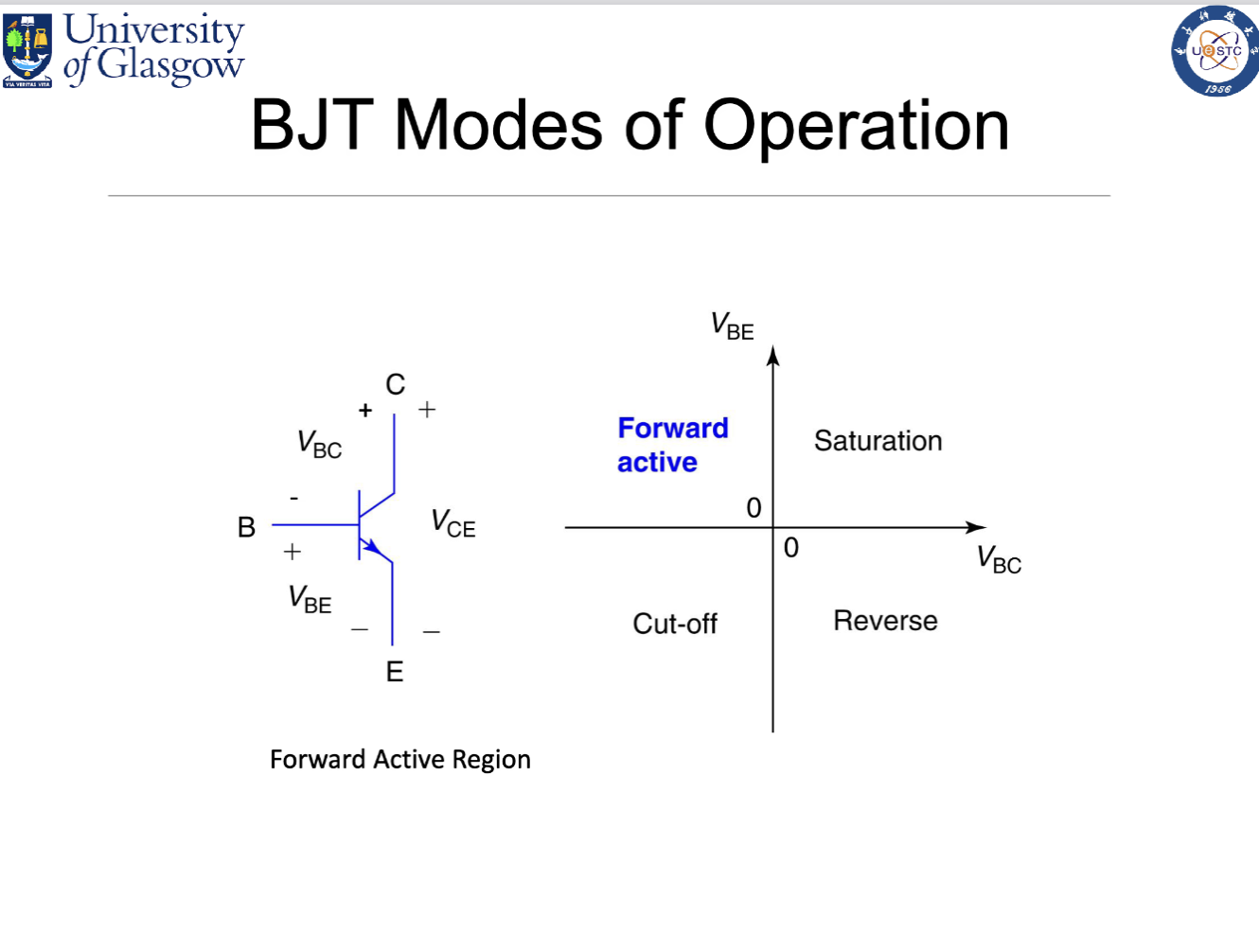
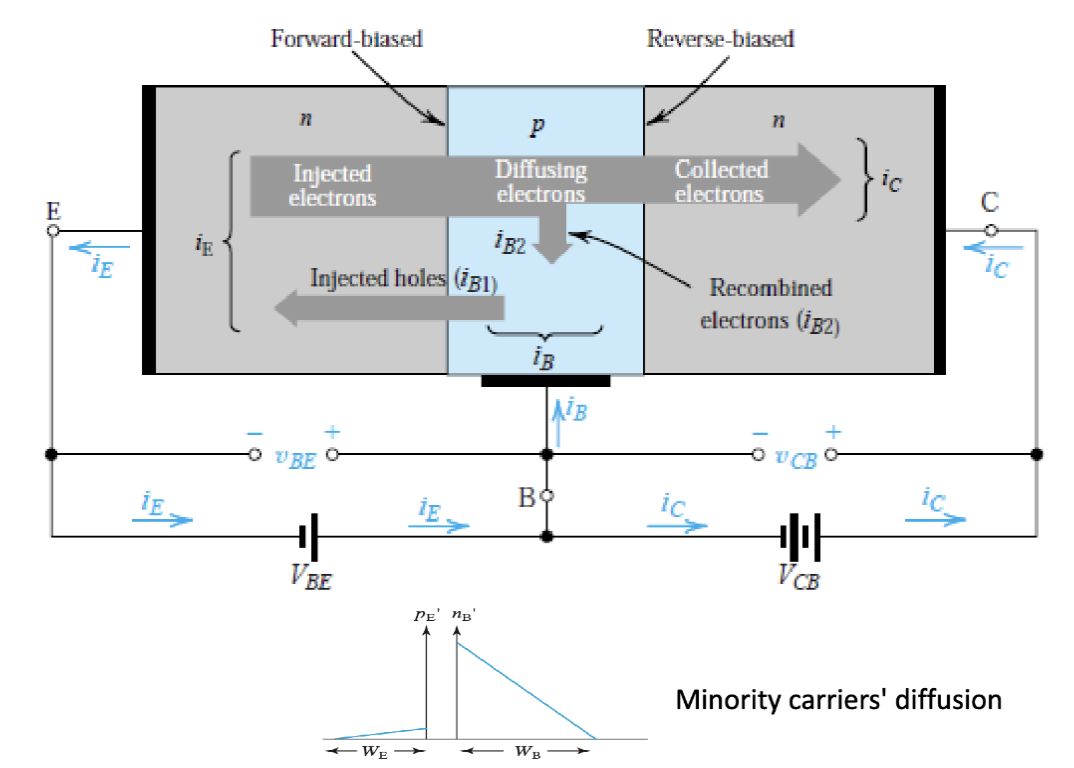
在正向放大过程中,电流从集电极流入,经过基极,最终流出发射极。基极电流 () 控制着集电极电流 () 和发射极电流 () 的大小。最终从发射极流出的电流是集电极电流和基极电流之和。
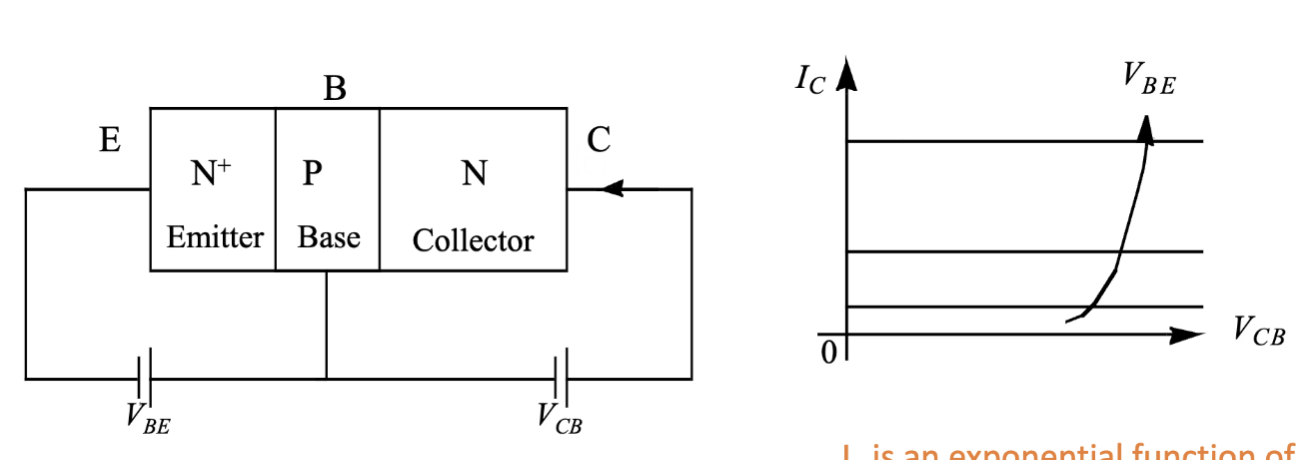
最终, ,也就是集电极电流大小是一个关于 的指数函数,而与 几乎无关。
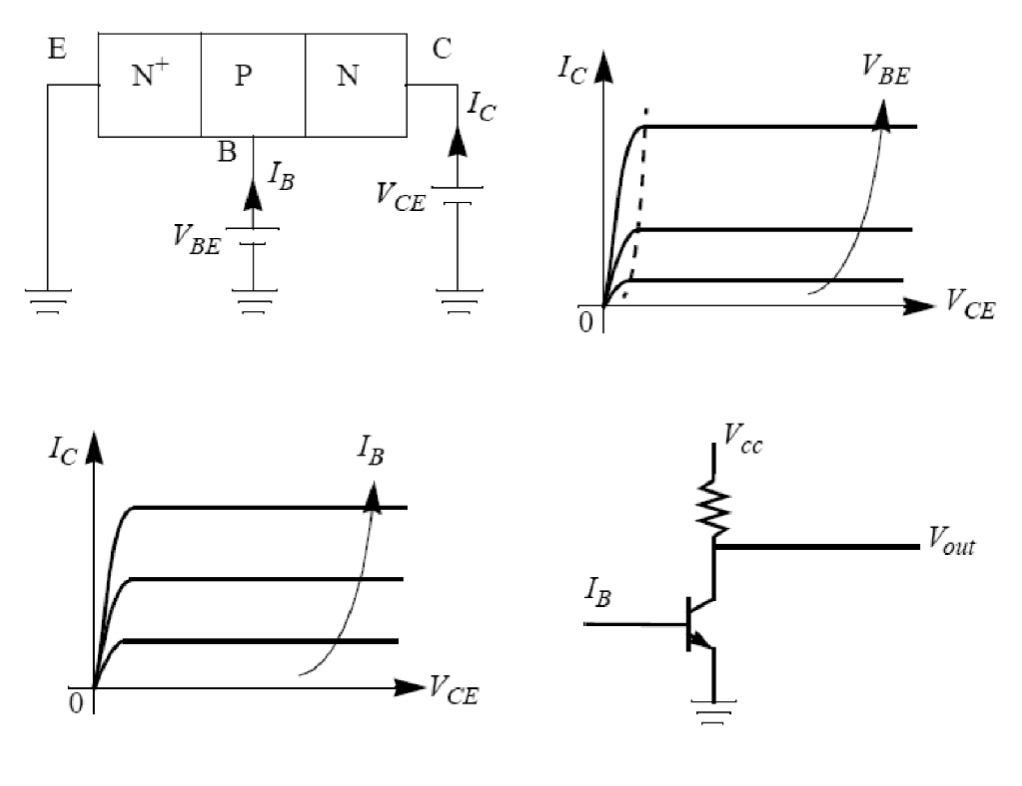
图上展示的是一种共发射极的配置。其中,发射极接地作为参考点,而基极和集电极的施加电压都是相对于发射极而言的。
可以发现,在 刚开始增长时, 会迅速增加,这个阶段称为“饱和区”。当 继续增加时, 会趋于平稳,这个阶段称为“放大区”或“线性区”。在这个区域内, 主要由 (或者说输入电流 ) 决定。在 继续增长到了一定程度后,晶体管进入“击穿区”, 会再次迅速增加。
电流 & 增益
集电极电流可以通过这个公式给出:
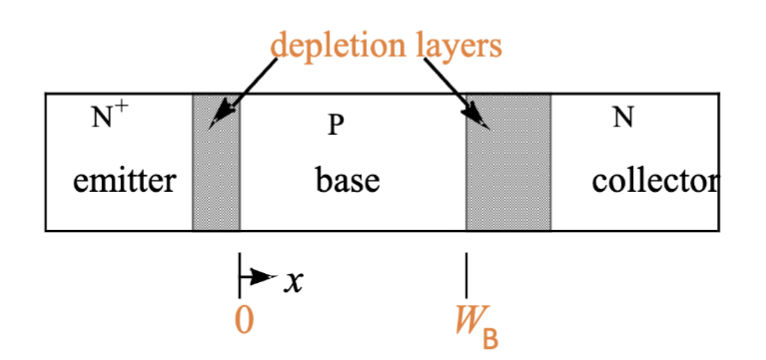
其中, 是基区的电子扩散系数, 是基区的宽度, 是基区的掺杂浓度, 是基区的本征载流子浓度, 是发射结的横截面积。
虽然主要电流是电子从发射极(N 区)流向基极(P 区),但同时也存在空穴从基极(P 区)注入到发射极(N+区)的现象。这些空穴必须由基极电源提供,因此它们构成了基极电流 的主要部分。
对于一个均匀的发射极,有:
其中, 是发射区空穴扩散系数, 是发射区宽度, 是发射区掺杂浓度。
观察一下 和 的表达式,可以发现二者似乎都与 成正比。因此,我们可以定义一个参数 ,表示集电极电流与基极电流之比:
这里的 称为共发射极电流增益 (Common-Emitter Current Gain),指的是集电极电流与基极电流之比。类似的,还有共基极电流增益 (Common-Base Current Gain) ,定义为:
将 和 的表达式代入 的定义,可以得到:
示例计算:
功耗
功耗的计算公式为 。对于 BJT,我们有不同的电流和电压需要考虑,总功率同时需要考虑 和 以及它们对应的电压:
因为有 ,并且通常 很大,集电极电流远大于基极电流,所以功耗主要由集电极部分决定。功率简化为
基极宽度调制
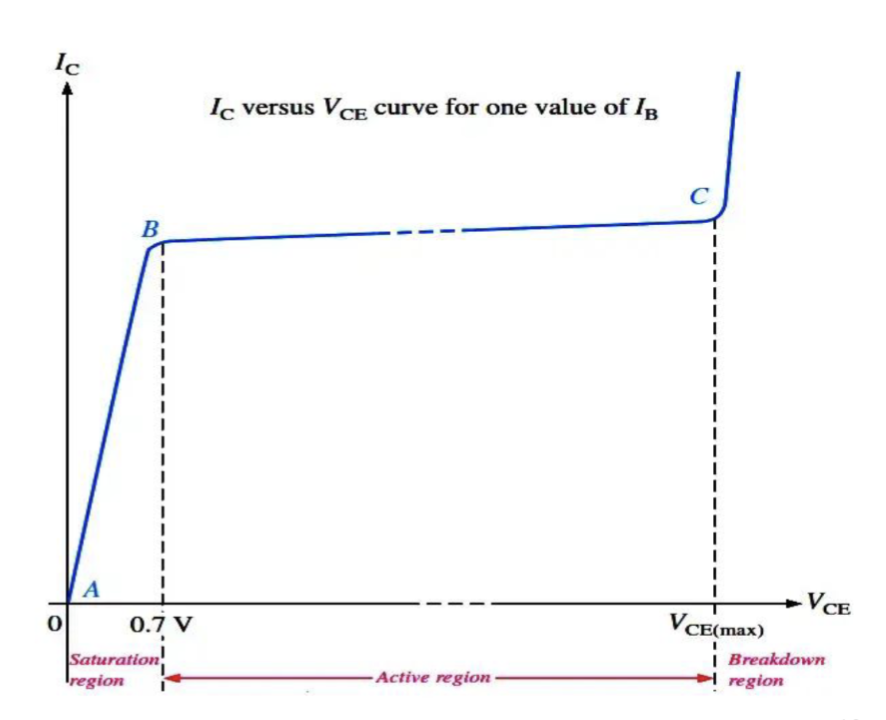
对于一个 BJT,还有一个重要的参数是他的输出电阻。图中是它的集电极电流 随着集电极-发射极电压 变化的曲线。
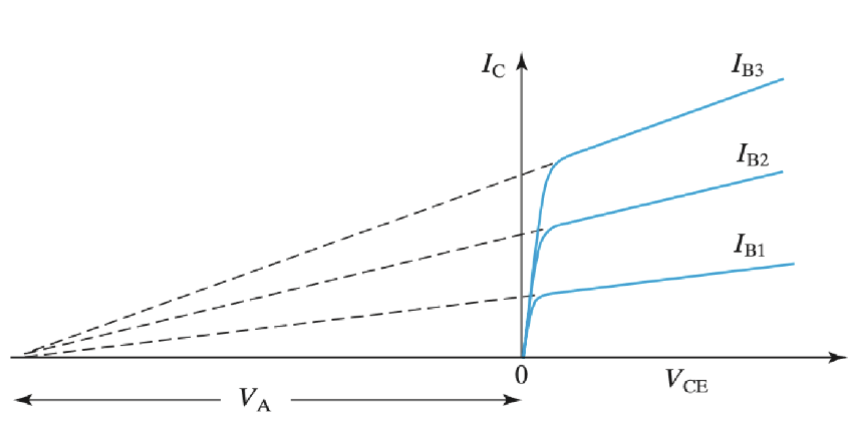
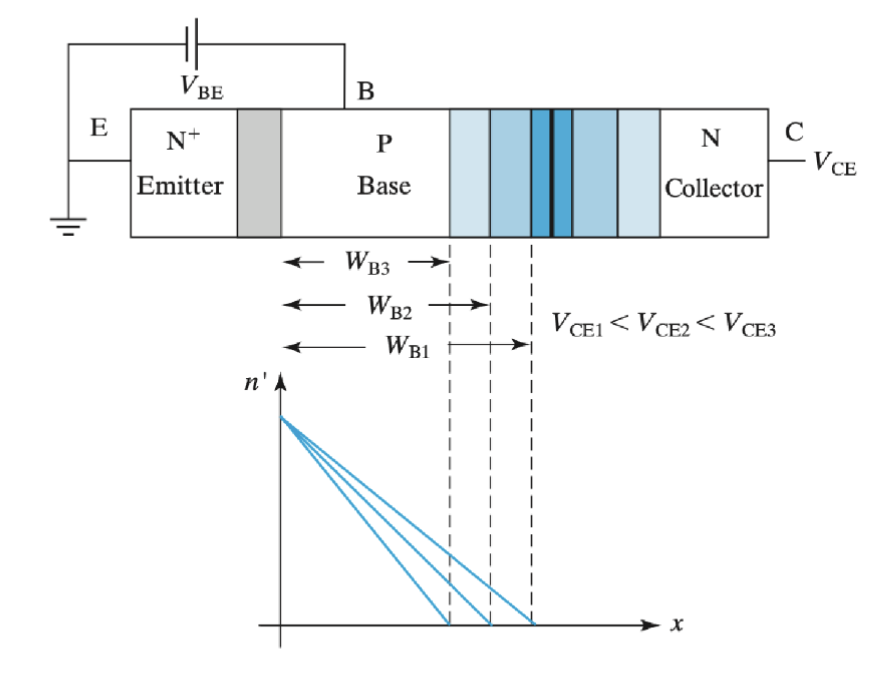
可以发现,在饱和区,其曲线可以近似看作一条直线,然后每条直线的反向延长线都与横坐标轴相交于一个点 。这代表当 BJT 工作在饱和区时,集电极电流 并不是完全不受 影响的,而是随着 的增加而略微增加。这种现象称为基极宽度调制 (Base Width Modulation),也被称为 “早期效应” (Early Effect)。这会给其引入一个输出阻抗。
在较大的电压增益的情况下,更大的 会带来更大的输出阻抗,从而提升整体增益,表现更好。
其具体的产生原因是,在集电极电压 增加时,集电结的反向偏置增大,导致集电结耗尽区宽度增加,从而使得基区有效宽度减小。基区宽度减小会导致更多的电子从发射极注入到集电极,从而增加了集电极电流 。
解决的方法有
- 增加基极宽度
- 增加基极掺杂浓度
- 减小集电极掺杂浓度
结型场效应晶体管 (JFET)
JFET 概述
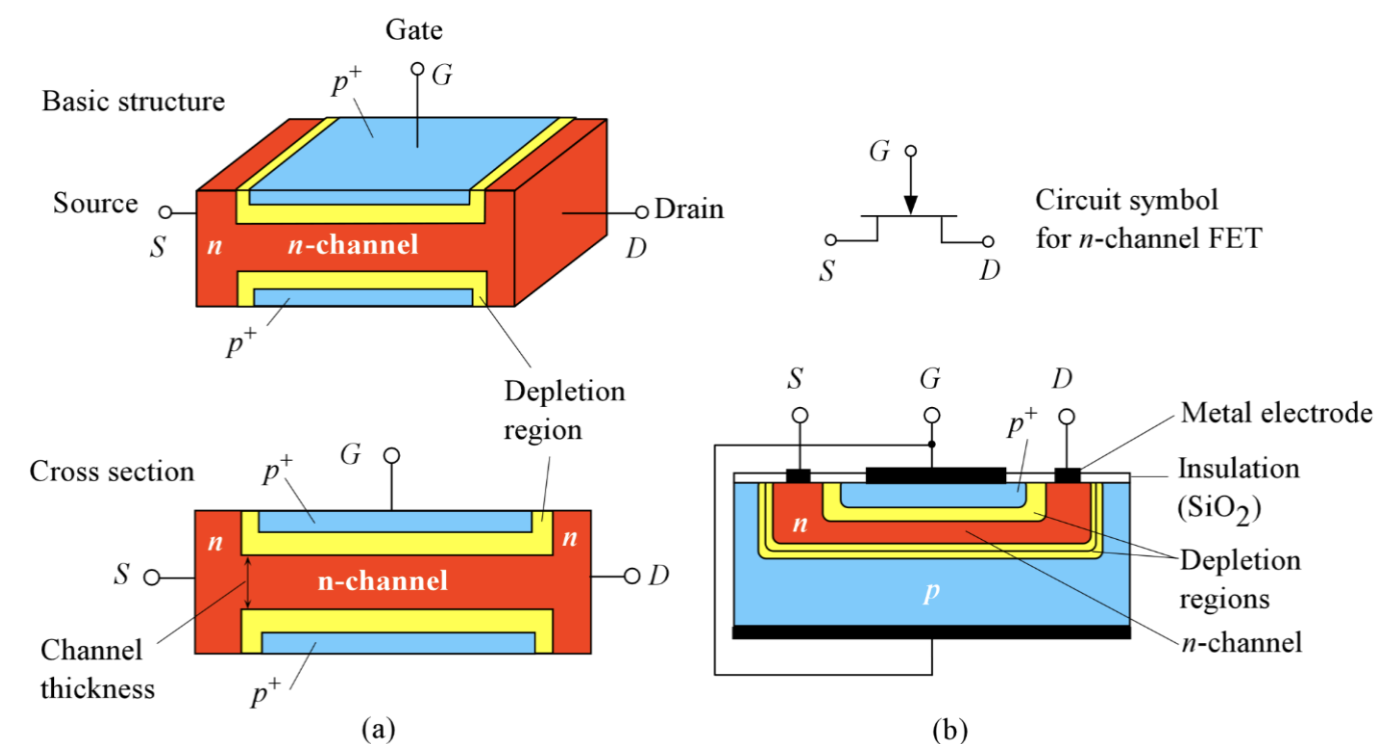
场效应管 (Field-Effect Transistor) 指的是通过电场效应来控制电流流动的电子器件。 JFET (Junction Field-Effect Transistor) 是最早被发明的场效应管类型之一。它由一个半导体通道和两个 PN 结组成,通过控制 PN 结的偏置来调节通道的电导,从而控制电流的流动。
FET 的分类如下图:
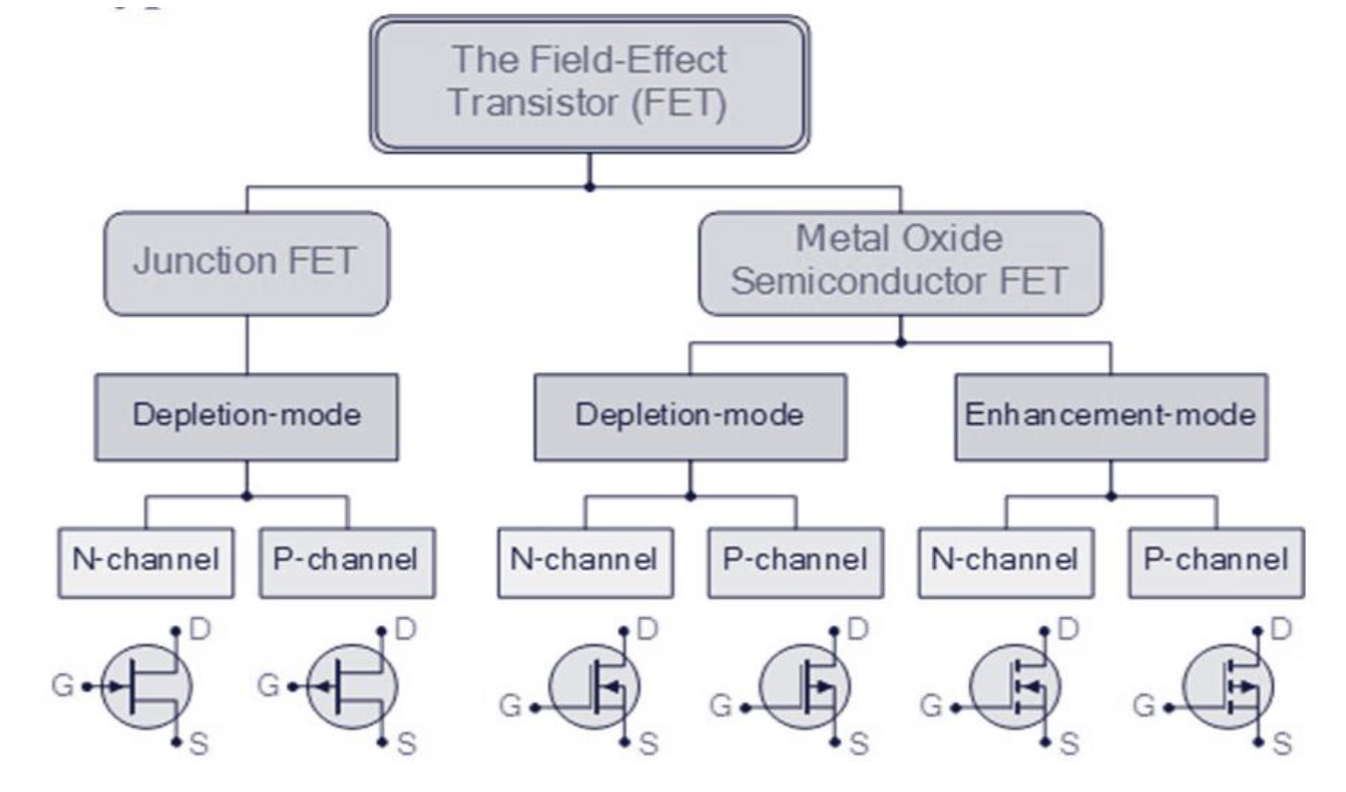
JFET 是一个三端口的压控半导体设备,可以用于控制开关或者放大器,电路符号和结构如图所示:
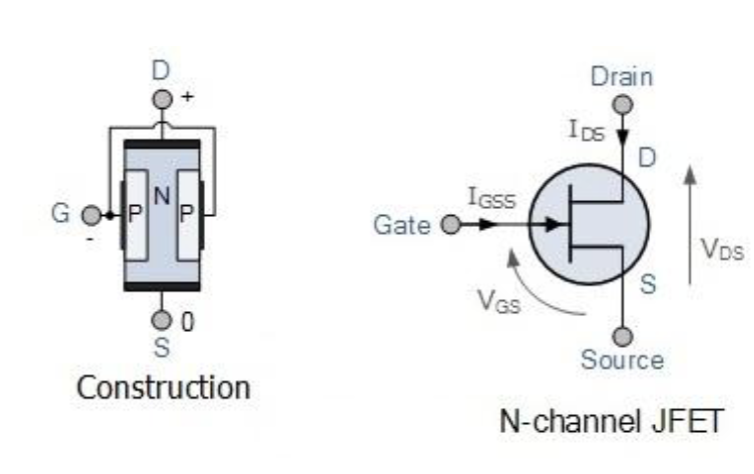
和 BJT 类似,JFET 的结构里有三个端口,两个 PN 结。对于常见的 n 沟道 JFET (n-channel JFET),其通道由 n 型半导体材料构成,两个 PN 结由 p 型材料形成。对于 p 沟道 JFET (p-channel JFET),则相反。
JFET 工作原理
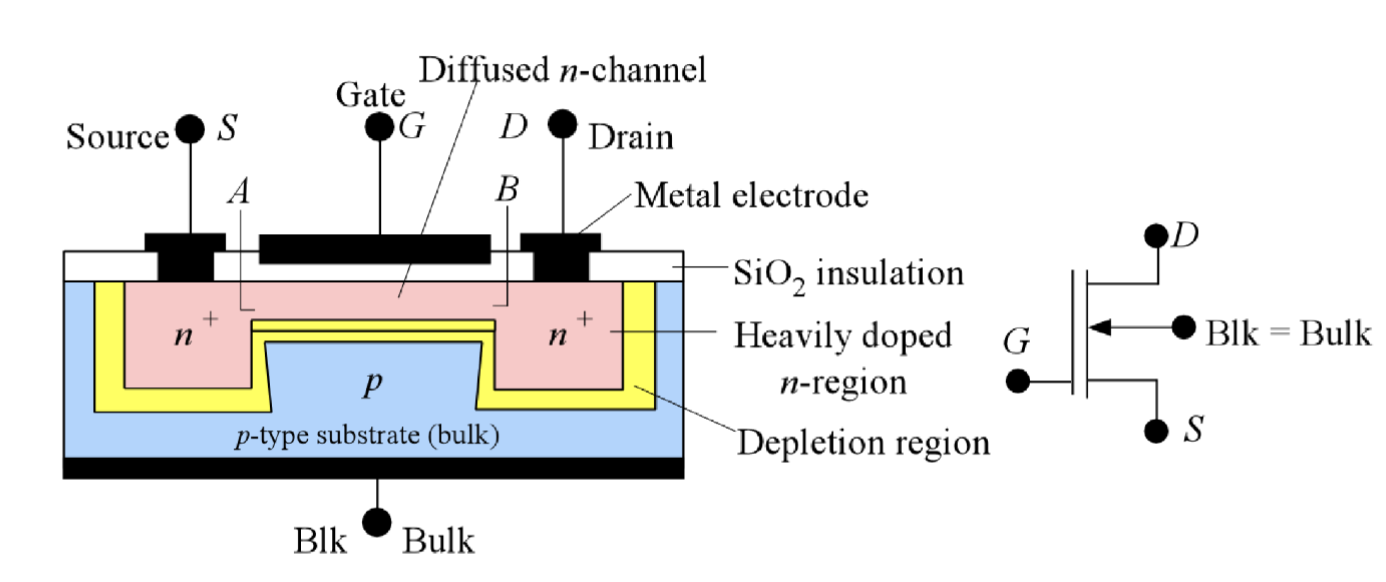
栅极不施加电压
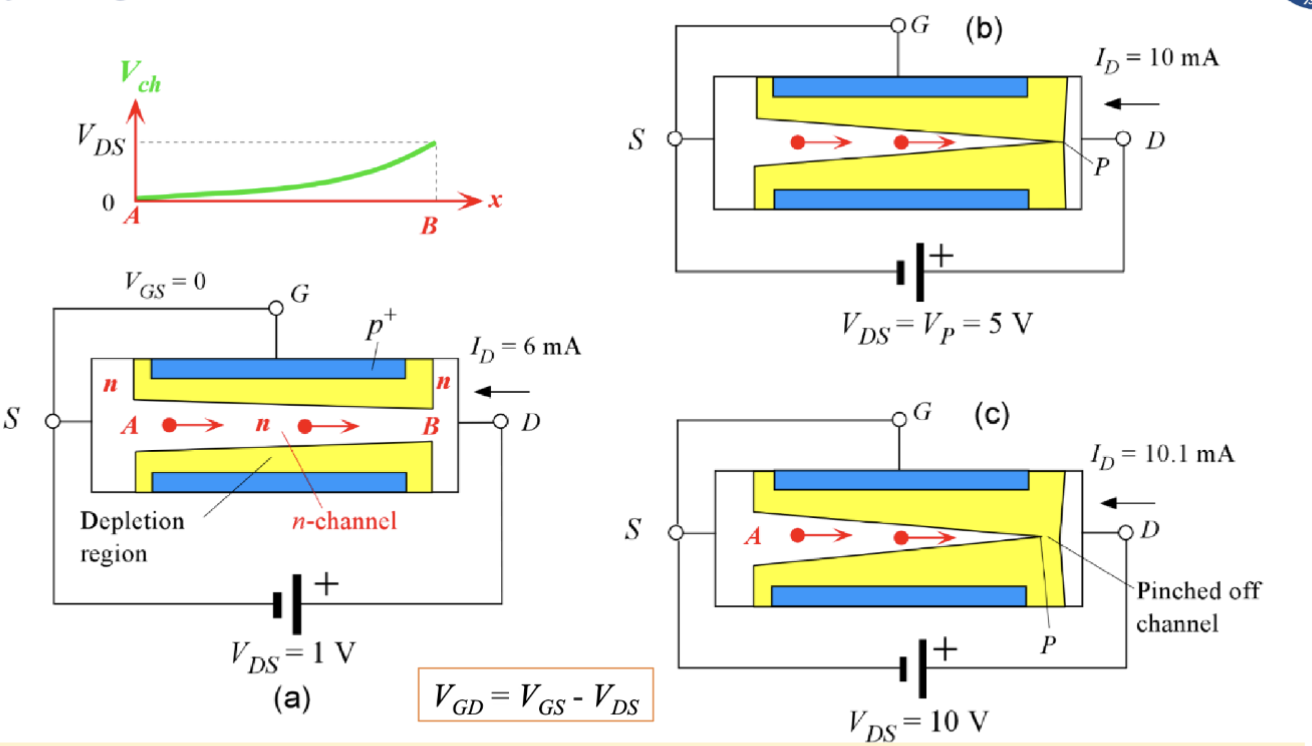
把源级设为参考电压,则在沟道内的不同位置,其内部点位的变化曲线如左上角的图所示。此时我们不在栅极上施加电压,在漏极上施加的电压越大,则两侧的耗尽层会越宽,沟道的有效宽度会变窄,从而限制了漏极电流 的增大。
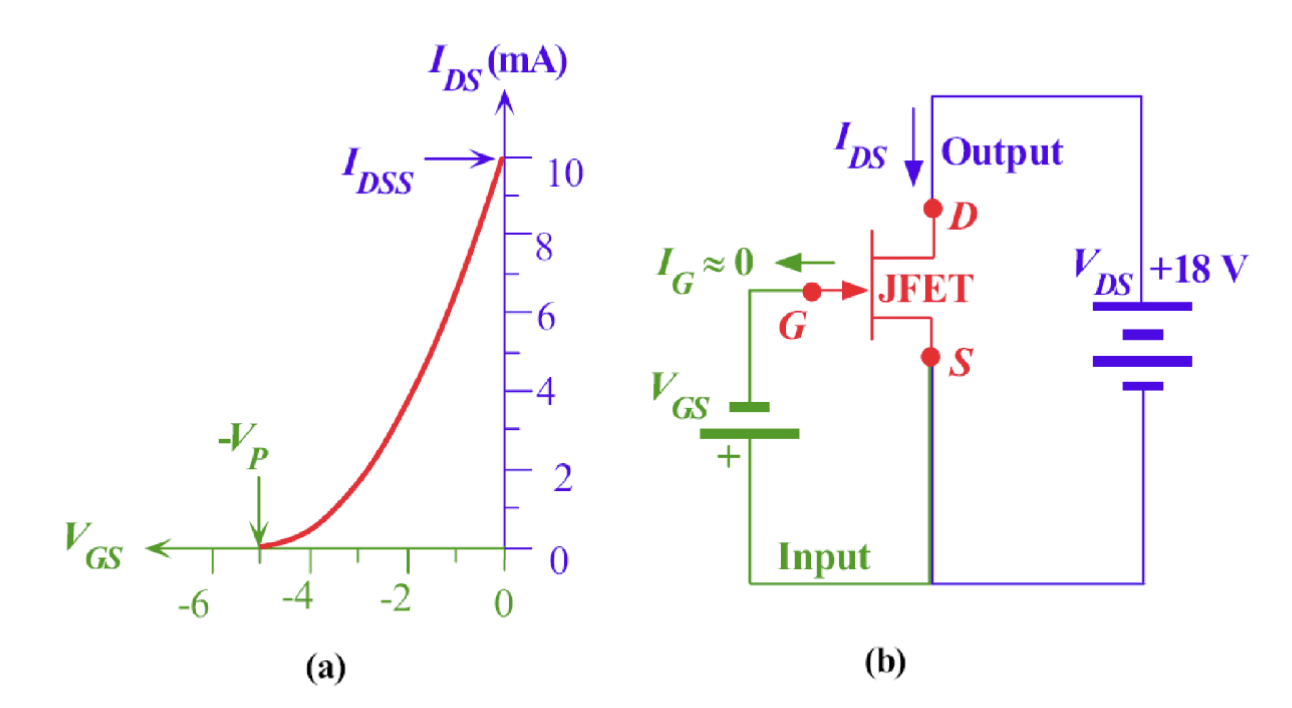
当漏极电压 增大到某个值 时,两侧的耗尽层会完全闭合,沟道被“夹断”,此时漏极电流达到最大值 ,之后无论如何增大 ,漏极电流都不会再明显增加,这个现象称为“钳位” (pinch-off)。
基于这个现象,我们定义在栅极电压为 0 的情况下的钳位电压:
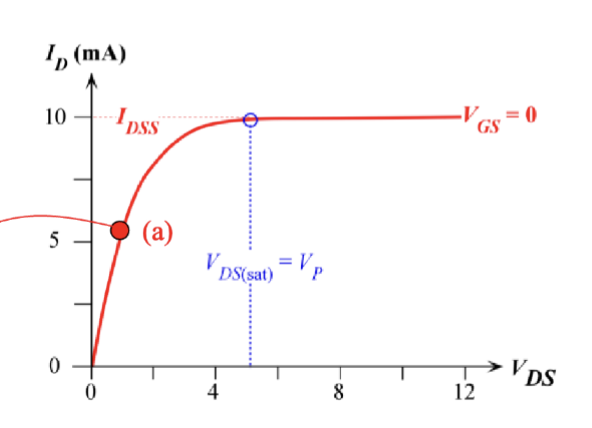
钳位的现象发生主要是因为大于 的那一部分电压基本都被增加的耗尽层所消耗掉了,导致实际加在沟道上的电压没有继续增加,因此漏极电流也不会继续增加。
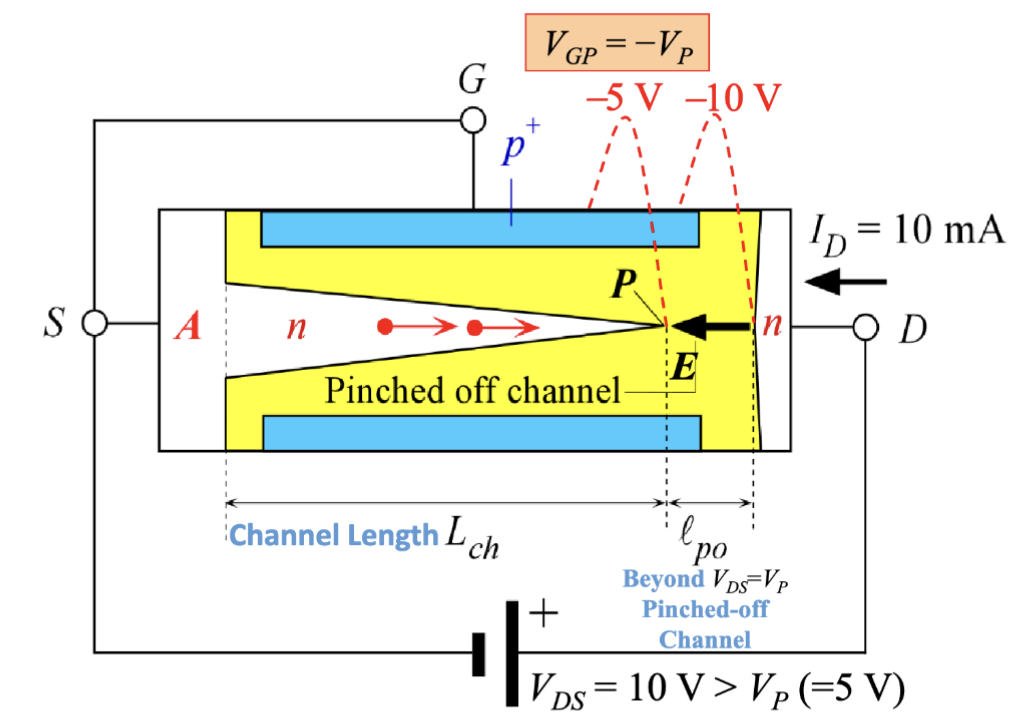
这个时候,N 沟道中的电子向 P 区漂移,到达 P 区时会被电场扫过夹断的沟道。这个过程类似于 BJT 的基区中的少数载流子行为。
此时的漏极电流实际上主要由 A 到 P 之间的导电 n 沟道的电阻 来决定,也就是
而 P 之后的区域因为载流子耗尽有很高的电阻吸收了大部分电压。
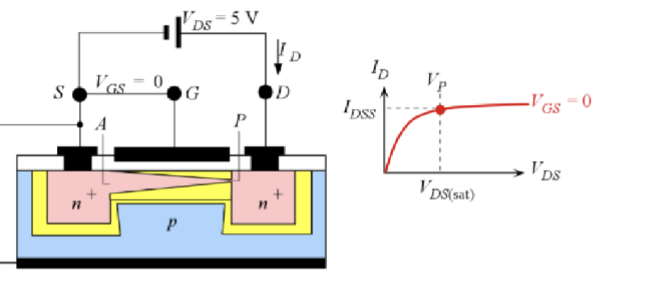
栅极施加少量电压
还是以源级作为参考电压,给栅极施加一个负的电压大小 。此时,耗尽区的宽度会变宽,从而进一步减小了沟道的有效宽度。在这种情况下,只用施加更小的漏极电压 就可以使沟道夹断,并且最终得到了更小的漏极电流 。
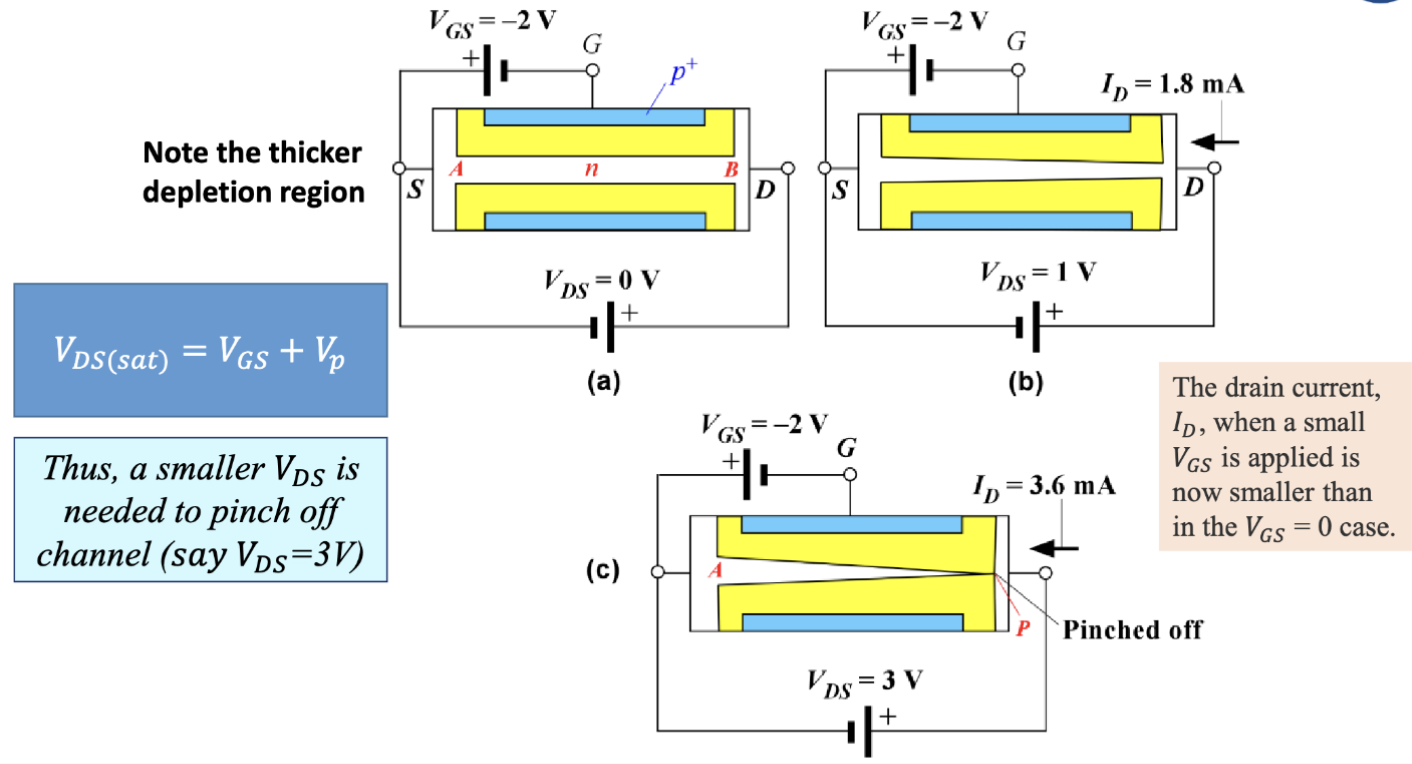
定量来说,几个电压之间的关系是
所以,图中在栅极施加的电压大小为 ,因此在漏极施加了 时沟道就被夹断了。
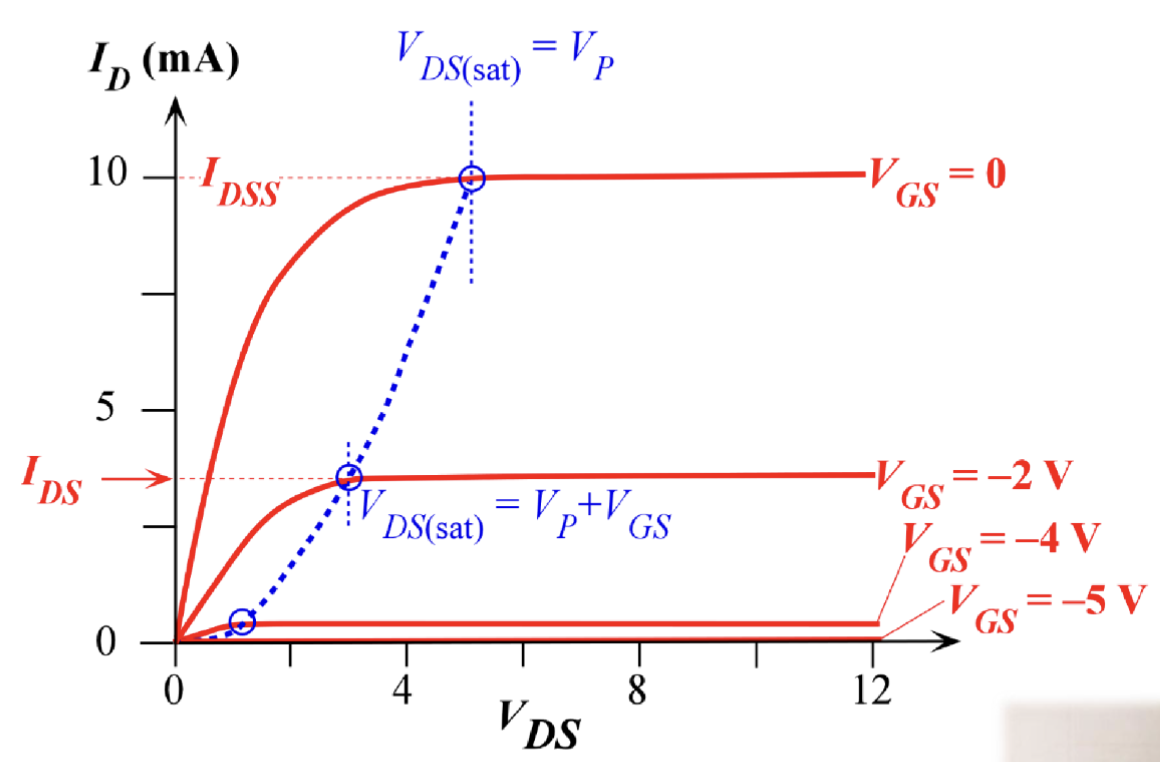
通过更改在栅极上施加不同大小的电压大小,我们可以控制漏极电流 的大小,最终如图所示
PPT 上给的类比例子是一个水龙头,漏极电压提供的是水源,然后栅极电压就像是水龙头的开关,通过调节水龙头的开合程度来控制水流的大小。
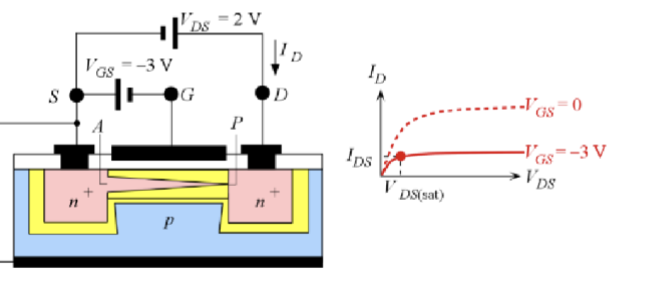
在施加了栅极电压后,沟道内部的电位分布有一点差异,如下图所示:
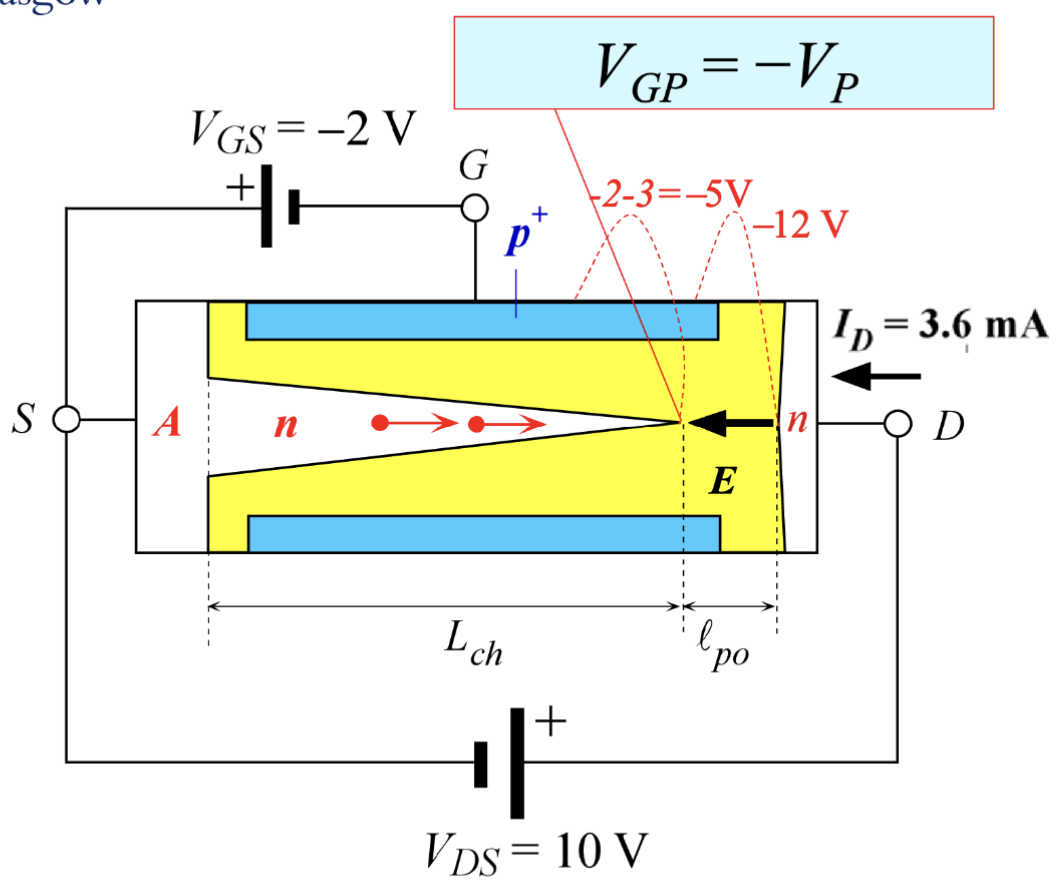
这次我们还是把沟道最终被夹断的点叫 P 点,此时 P 点的电位大小并不是之前的 ,而是 。因此,漏极电流可以表示为:
这里 是施加的栅极电压, 是 N 沟道的 A 到 P 点的有效电阻,这里的括号的意思是这个电阻会随着栅极电压的变化而变化,是一个函数。
随着栅极电压在负向增大,增加了 PN 结的反向偏置,沟道宽度会更窄,进而电阻会变得更大;同时, 也会变小。因此,漏极电流 会随着栅极电压的负向增大而减小。这两种效应同时作用,使得漏极电流 几乎随着 的增大而抛物线式减小 (parabolically decreasing)。
栅极施加关断电压
如果我们在 上施加一个足够大的电压,比如 ,此时不在漏极上施加电压,则两个耗尽层在整个沟道长度上都相互接触,整个沟道都被关闭了。
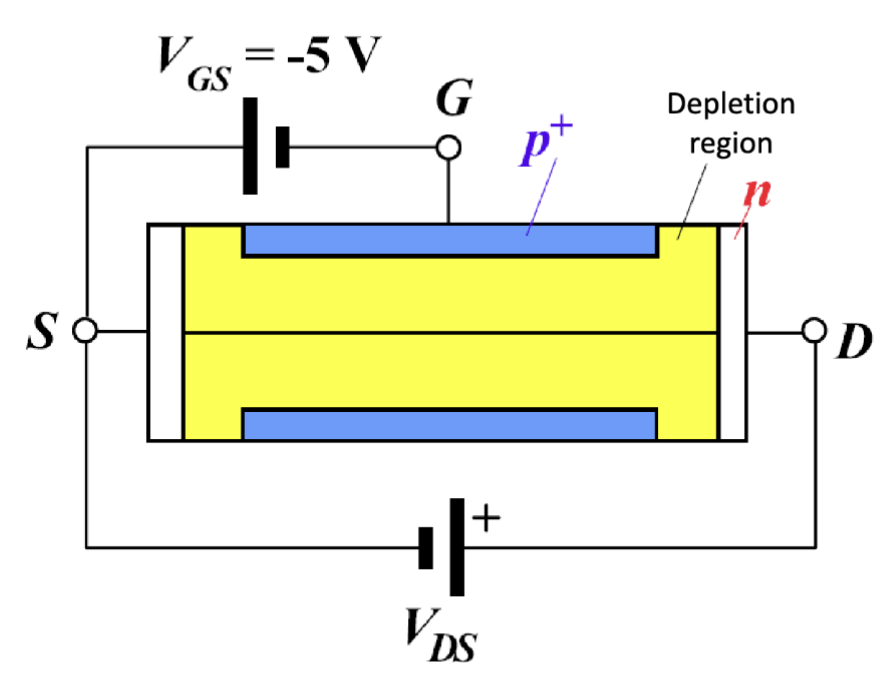
当我们施加 时,流过的电流只由耗尽层中的热生载流子产生,非常的小。根据下图也可以看出,在 时,漏极电流 几乎为零。
图中的 的一个简单计算公式为
这里的 是在 时的漏极电流, 是使得漏极电流接近于零的栅极电压,也就是 。
JFET 共源放大器
我有模电 PTSD .jpg
JFET 中的晶体管作用是通过 来控制 的大小,因此我们可以通过调节 来实现放大器的功能。在这种放大器中,输入信号是包含 的栅源电路,输出电路是漏源电路,由漏极电流 驱动。这种构型因为源极作为输入和输出的公共端口,所以称为共源放大器 (Common-Source Amplifier)。
JFET 不常用 PN 结的正向偏置,输入基本都是负电压,所以输出的最大电流只有 。常见的构型如下图所示:
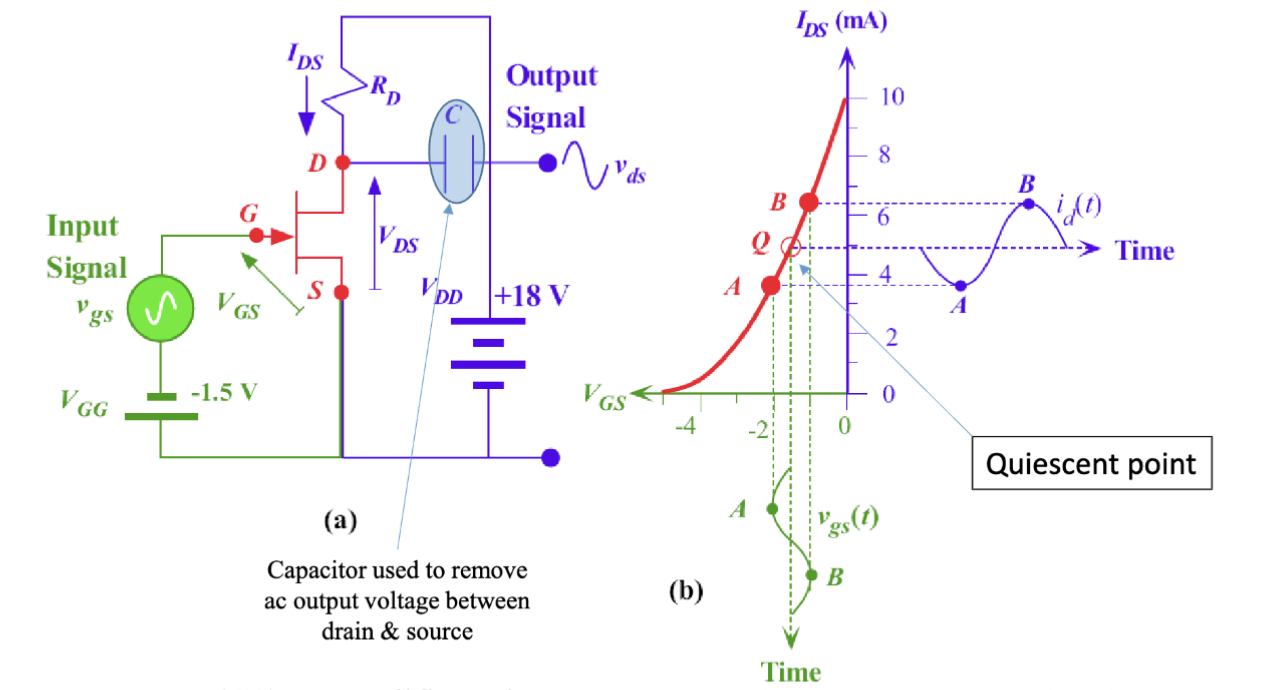
又到了我最喜欢的小信号模型环节。输入信号接在了栅极上,有一个 的偏置电压,漏极上有一个 的电源。漏极串联了一个电阻 ,最终输出的电压是 ,通过一个电容过滤直流分量。
我们之前有得出过这个公式。
在小信号模型下,对静态工作点附近进行线性化处理,可以得到漏极电流增量和栅源电压增量之间的关系:
但是,这个情况中输入信号的幅度大小为 ,还是很大,不能忽视非线性成分。在实际的仿真中还是可以发现上下幅度不一致,这是因为线性近似只在小范围内有效,幅度过大时会引入非线性失真。

最终,对于这个放大器,仿真的电压增益为
负数增益意味着输出信号和输入信号是反相的。
增大电阻大小 可以增大电压增益,但是始终需要保证 不低于 ,否则晶体管会进入饱和区,失去放大作用。
当信号相对于直流值较小时,可以用微分表示小信号。在这种情况下, 引起的 可以表示变化可以用于定义 JFET 的互导 ,也就是我们之前提到的小信号模型中的 。
还有我们之前推导的
类似的,定义小信号模型中的电压增益
结论也符合我们之前的分析:增大漏极电阻 可以增大电压增益 。
练习题略
金属氧化物场效应管 (MOSFET)
原来人们所说的遇见宿敌的感觉就是这个感觉,模电还是伤我太深了
你是……不能忘记的人
MOSFET 概述
和之前的 JFET 部分类似,MOSFET 是另一种 FET 的实现方式,其使用的是金属-氧化物-半导体结构来控制电流的流动。MOSFET 广泛应用于数字电路和模拟电路中,因其高输入阻抗和低功耗特性而受到青睐。MOSFET 还有别的简写,比如
- MOST (Metal-Oxide-Semiconductor Transistor, 金属-氧化物-半导体晶体管)
- IGFET (Insulated-Gate Field-Effect Transistor, 绝缘栅场效应晶体管)
- MISFET (Metal-Insulator-Semiconductor Field-Effect Transistor, 金属-绝缘体-半导体场效应晶体管)
- …
现代的集成电路通常有几十亿个晶体管,而其中绝大多数都是 MOSFET。
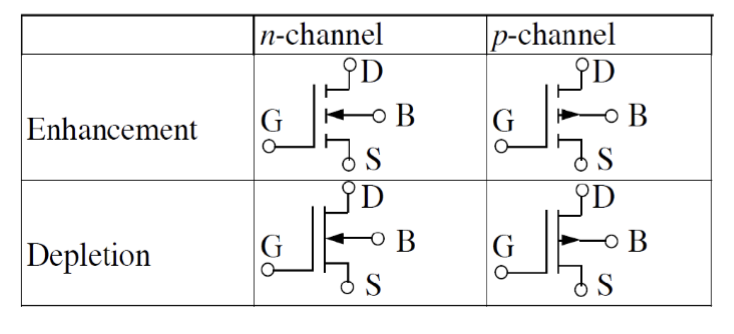
MOSFET 可以分为 N 沟道 (n-channel) 和 P 沟道 (p-channel) 两种类型,分别对应电子和空穴作为主要载流子。其电路符号如下所示:
| 沟道类型 | 载流子 | 源极和漏极掺杂 | 衬底掺杂 |
|---|---|---|---|
| N 沟道 MOSFET | 电子 | N 型 | P 型 |
| P 沟道 MOSFET | 空穴 | P 型 | N 型 |
其中,又可以以默认状态分为两种类型:
- 增强型 MOSFET (Enhancement MOSFET):默认状态下沟道不存在,需要通过在栅极施加电压来形成导电通道。
- 耗尽型 MOSFET (Depletion MOSFET):默认状态下沟道存在,可以导通电流,通过在栅极施加电压来调节沟道的导电性。
组合一下这两种分类,我们可以得到四种不同类型的 MOSFET:
MOSFET 工作原理
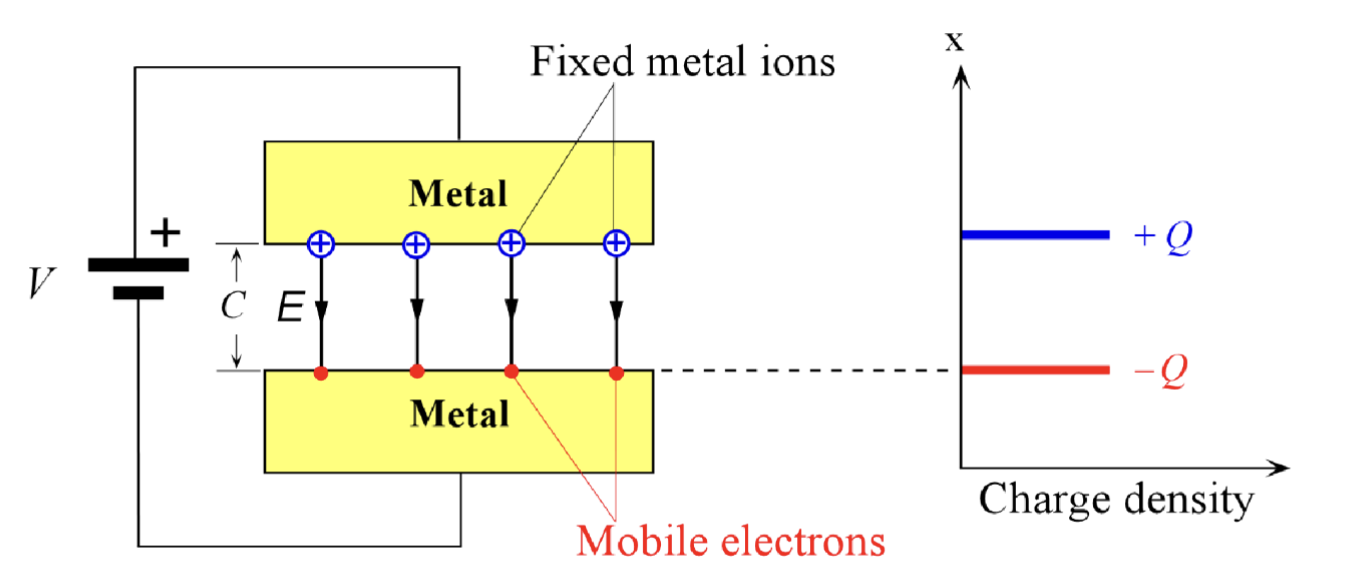
两个由绝缘体隔开的金属板可以看作一个电容,在这金属板上面施加电压会让金属板上积攒电荷,并在两块金属板之间产生电场。金属-空气-金属这种电容器中,电荷都位于金属表面,电厂不会穿透金属内部,这是因为金属内部有大量自由电子,这些电子会重新分布以抵消电场。
在最终状态,两块金属板之间的电势差等于施加在两块金属板上的电压。如果我们把电势较低的那块金属板换成 p 型半导体,那么电场就会穿透半导体表面的一定深度,这个深度取决于施加的电压大小以及半导体的掺杂浓度。因为表面的负电荷受体数量不足以产生足够的负电荷到 。因此,一定量的内部的负受体被暴露出来。
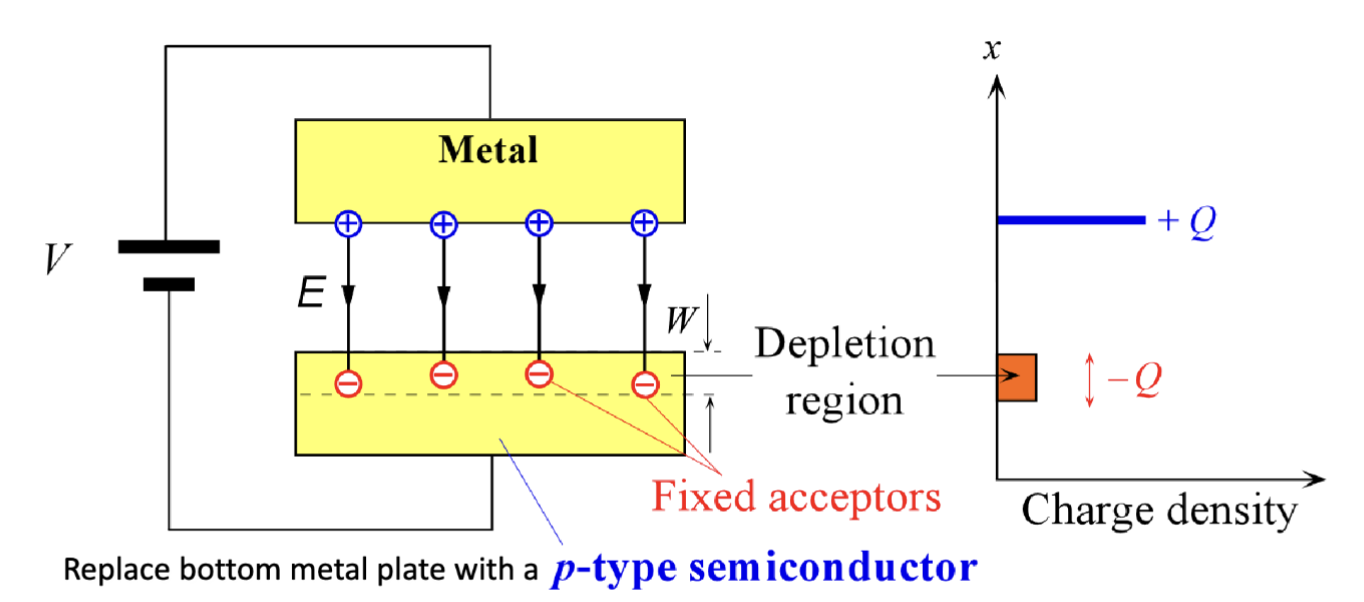
在这个过程中,在金属上施加的正点压会让带正电的空穴远离表面,形成一个耗尽层,进而暴露出一个没有载流子的区域。这个区域中主要含有固定的带负电的受主离子。因此,电场穿透的区域相当于耗尽了其平衡浓度的空穴。
耗尽层的宽度可以通过这个公式计算
其中, 是金属板上积攒的电荷量, 是金属板的面积, 是耗尽层的宽度, 是 p 型半导体中受主杂质的浓度。
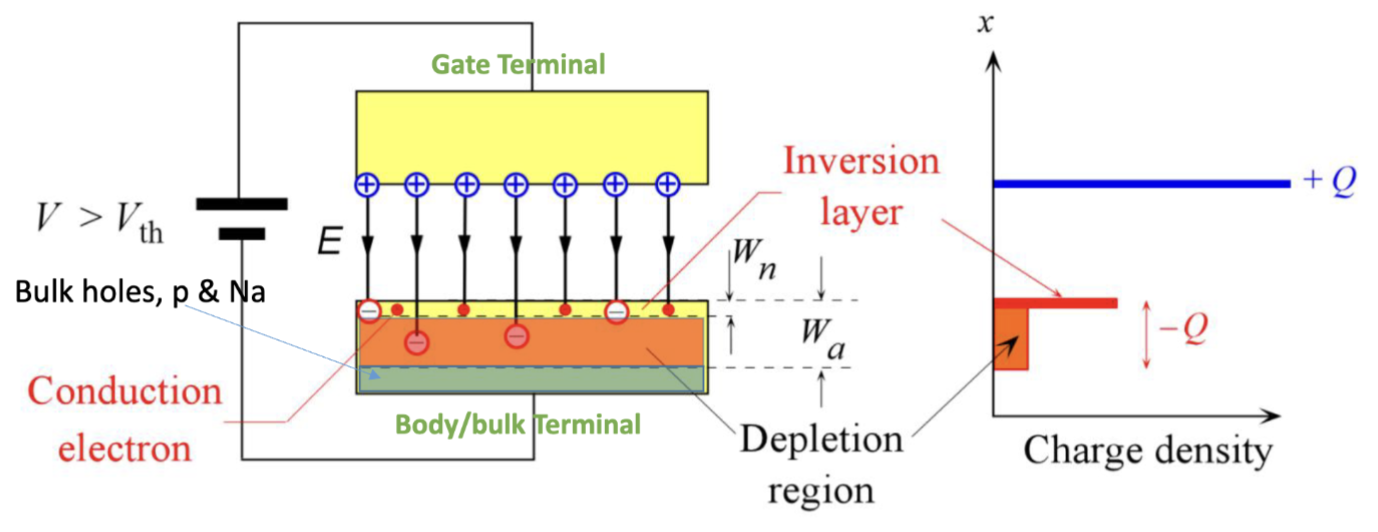
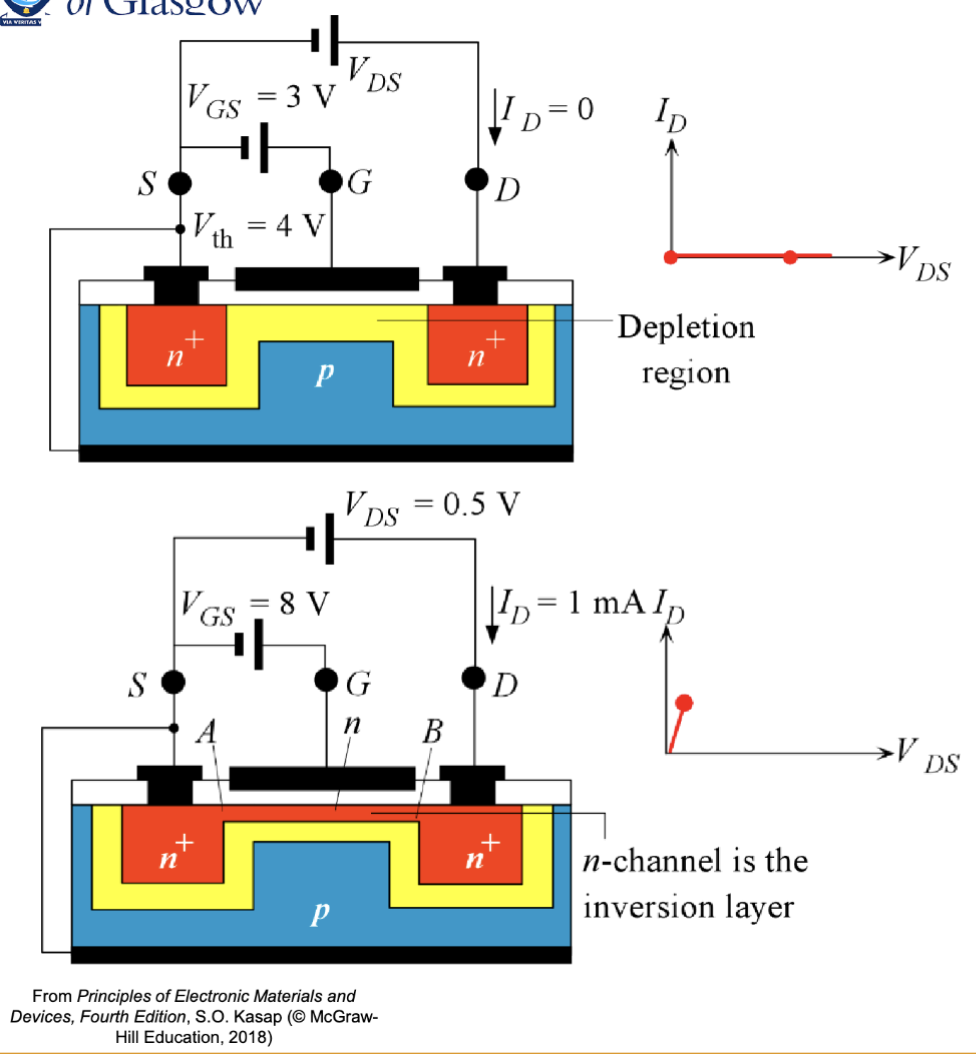
当电压足够高时,半导体和绝缘体之间的界面会出现一个高浓度的负电荷载流子反型层 (Inversion Layer). 这个反型层的形成是因为在高电场下,半导体内部的热激发电子会被吸引到界面处,形成一个富含电子的区域,这个区域的电子浓度甚至可以超过空穴浓度,从而实现了载流子的反转。
一般把反型层中的电子密度和衬底中的空穴密度相等时,外加的电压称为阈值电压 (Threshold Voltage) 。当有外加电压 时,反型层就会形成。
这对应的就是 MOSFET 的导通原理,上面的金属板连接的就是 MOSFET 的栅极 (Gate)。其还有两个电极,分别是源极 (Source) 和漏极 (Drain),分别连接到独立的高掺杂区域。这两个极的掺杂方式相同,和衬底的掺杂方式相反。
下图就是一个典型的 MOSFET 结构图。这是一个 NPN 型的 MOSFET,源极和漏极都是 N 型掺杂,而衬底是 P 型掺杂。我们称这个叫做 NMOS。
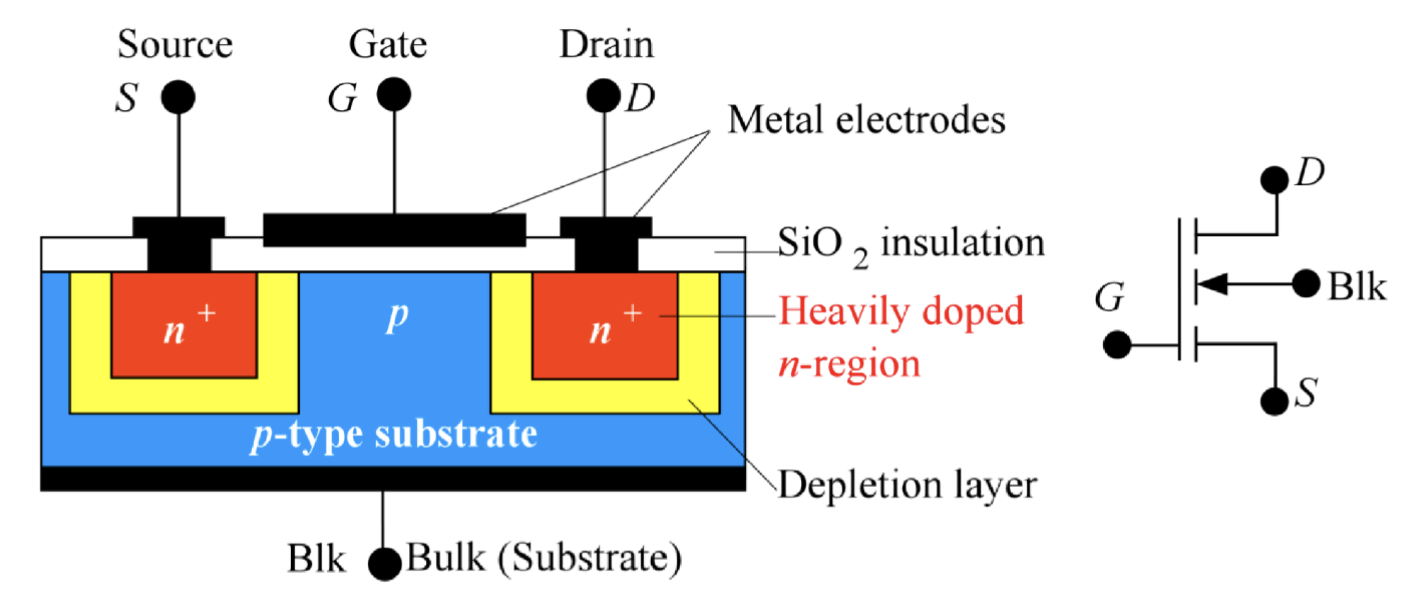
这里的源极和漏极的掺杂标注的是 “n+”,表示其掺杂浓度非常高,远高于衬底的掺杂浓度。这样做的目的是为了确保源极和漏极区域有足够的载流子,以便在 MOSFET 导通时能够提供足够的电流。对应的,如果是 PMOS,则分别是 “p+” 和 “n”。
源极叫做源极,是因为它是载流子的源头,在这里载流子是电子;漏极叫做漏极,是因为载流子从这里流出。所以,在 NMOS 中,源极连接到较低电位(通常是地),而漏极连接到较高电位。
MOSFET 的伏安特性
增强型 MOSFET (Enhancement MOSFET)
之前我们演示的就是一个典型的增强型 MOSFET。他叫增强型,因为给栅极施加的电流可以增强源极和漏极之间的导电能力。
其在栅极施加的电压大小 小于阈值电压 时,两个 “n+” 掺杂的源极好漏极之间还是被耗尽区间隔,可以看作一个开路状态,没有电流流过。当施加足够大的正电压 时,反型层形成,源极和漏极之间形成一条导电通路,电流可以流过。在漏极电压 比较小时,漏极的电流大小就是
在这一区域内,可以认为漏极电流随着漏极电压的增大而线性增大,这个区域叫做线性区 (Linear Region)。
在 变大的过程中,B 点点电压 逐渐减小,在漏极附近的反型层灰逐渐变窄,沟道电阻 逐渐增大。最后,当 减小到阈值电压 时,沟道在漏极附近被夹断。此时, 达到了饱和值 ,。
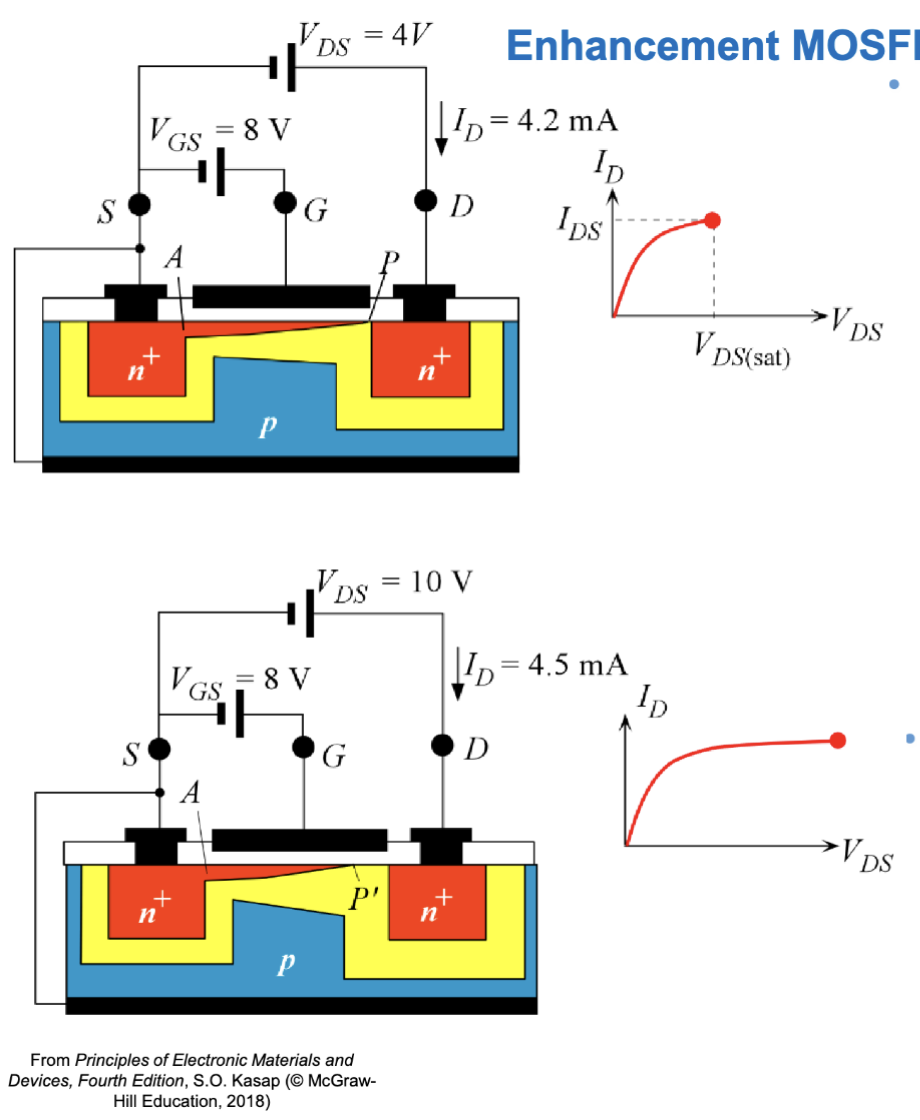
当 继续增大时,增加的电压大小被 P’ 之后当耗尽层吸收,漏极电流 不再增大,进入饱和区 (Saturation Region)。在这个区域内,漏极电流近似为常数,可以表示为
把两个区域综合起来,NMOS 的漏极电流的图像如下所示:
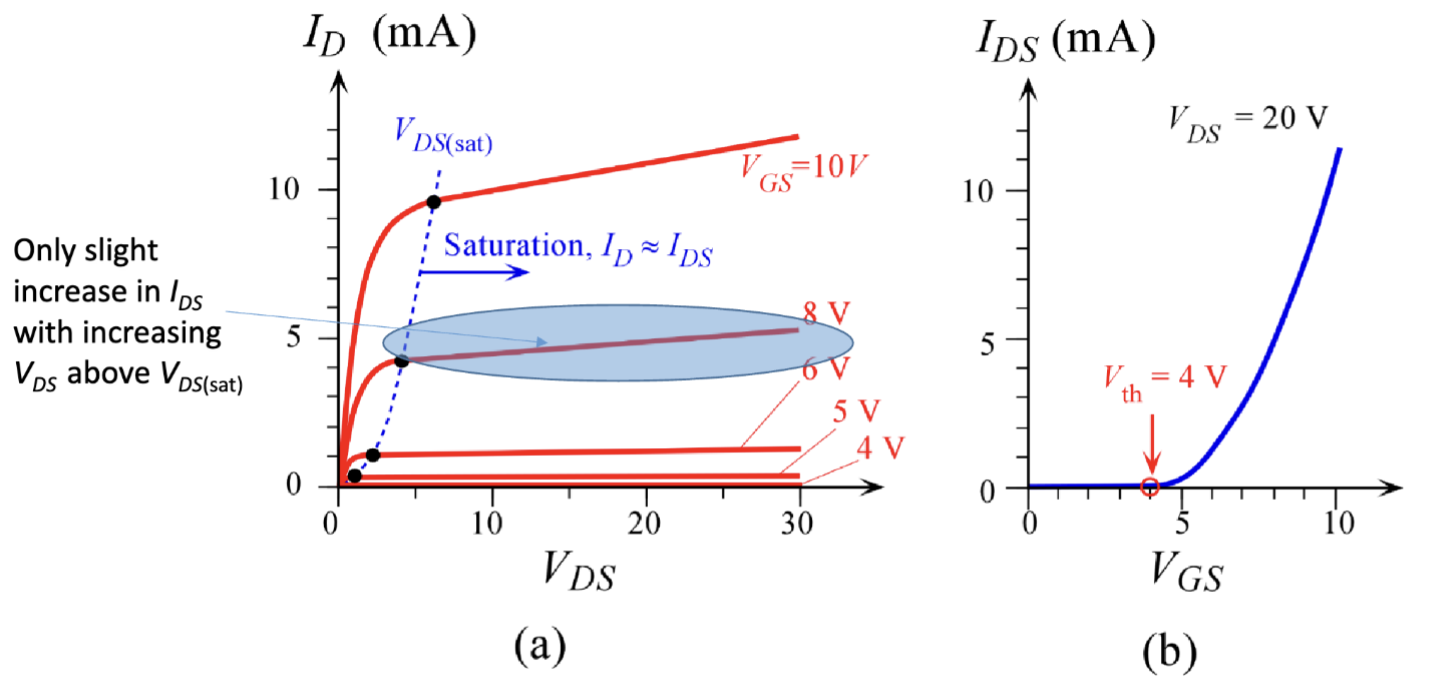
之后,线性区的漏极电流可以表示为
其中, 是电子的迁移率, 是氧化层的厚度, 是沟道的宽度, 是沟道的长度, 是氧化层的介电常数。最终算出来的 成为工艺参数 (Process Parameter),它和具体的制造工艺有关。
而饱和区的漏极电流可以表示为
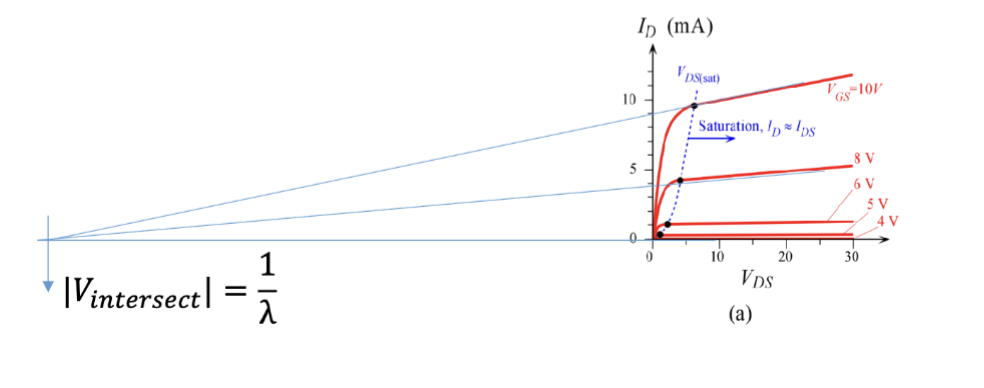
和 JFET 类似,这里的 是沟道长度调制参数 (Channel Length Modulation Parameter),表示沟道长度变化对漏极电流的影响,典型大小为 。其与横轴相交于 处。
所以,对于共源放大器的小信号模型的情况,其跨导参数可以表示为
这里的 称为过压 (Overdrive Voltage),表示栅极电压超过阈值电压的部分。之后,电压增益大小为:
耗尽型 MOSFET (Depletion MOSFET)
耗尽型 MOSFET 和增强型 MOSFET 不同,其是一个常开的设备,而增强型是常关的。耗尽型 MOSFET 的电路符号右侧是一条连续的线而不是三条断开的线。在掺杂结构上,耗尽型 MOSFET 的沟道区域本身就是掺杂好的导电通道,而不是通过栅极电压来形成的反型层,和 JFET 类似。
当不在栅极上施加电压时,耗尽型 MOSFET 的沟道已经存在,源极和漏极之间可以导通电流。其电流 和漏极电压 的关系如下图所示,先上升,在 达到饱和值 后沟道被夹断,进入饱和区,饱和电流为 。
以源极为参考电压,给栅极施加负电压,则沟道出现一部分耗尽区,宽度变窄,电阻升高。 饱和得更快,饱和电流减小。如图所示:
当给栅极施加正电压时,正点压的效果可以抵消一部分漏极电压带来的夹断,进而延迟饱和的到来,饱和电流增大。如图所示:
互补 MOSFET (CMOS)
基于 MOSFET 的伏安特性,MOSFET 的一个典型应用场景时作为开关使用。逻辑电路中,高电平为逻辑 1,低电平为逻辑 0。当栅极电压为高电平时,MOSFET 导通,源极和漏极之间形成导电通路,相当于闭合开关;当栅极电压为低电平时,MOSFET 截止,源极和漏极之间没有导电通路,相当于断开开关。比如这个构型
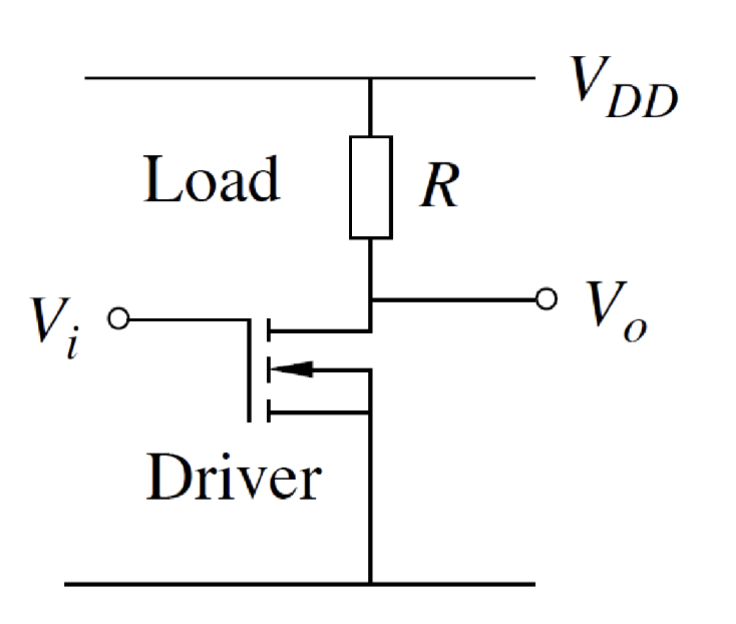
其中,R 的典型值大小为 $1M\Ohm$。 当输出低电平的时候,驱动器开启,直流电流较大,这会导致显著的功耗。目前的数字电路设计中,通常使用互补 MOSFET (Complementary MOSFET, CMOS) 技术来实现低功耗的逻辑门电路。CMOS 技术结合了 NMOS 和 PMOS 晶体管的优点,通过互补的工作方式来减少静态功耗。
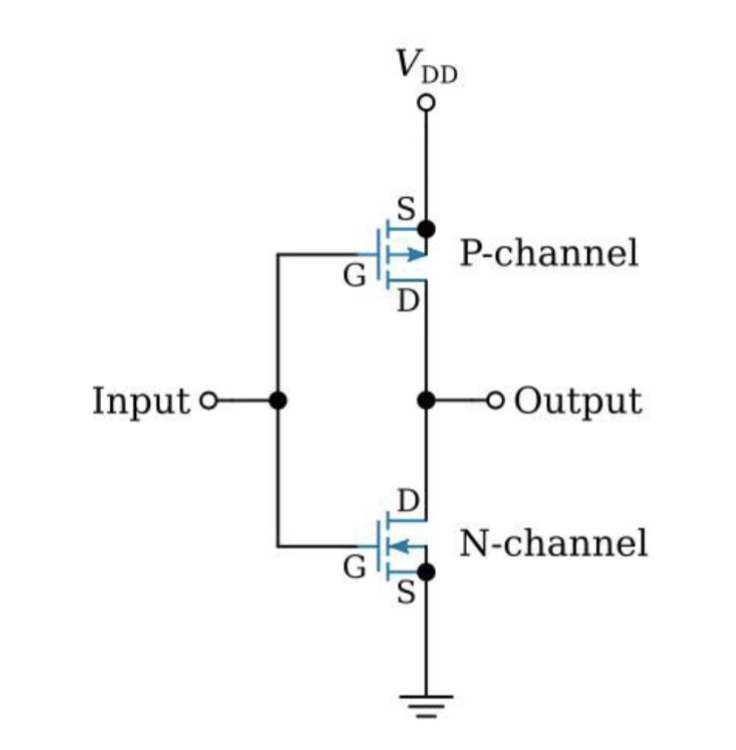
CMOS 就是把一个 PMOS 和一个 NMOS 组合在一起使用。当输入为高电平时,NMOS 导通,PMOS 截止,输出被拉到低电平;当输入为低电平时,PMOS 导通,NMOS 截止,输出被拉到高电平。这样,在稳态下几乎没有直流电流流过,从而实现了低功耗的逻辑操作。
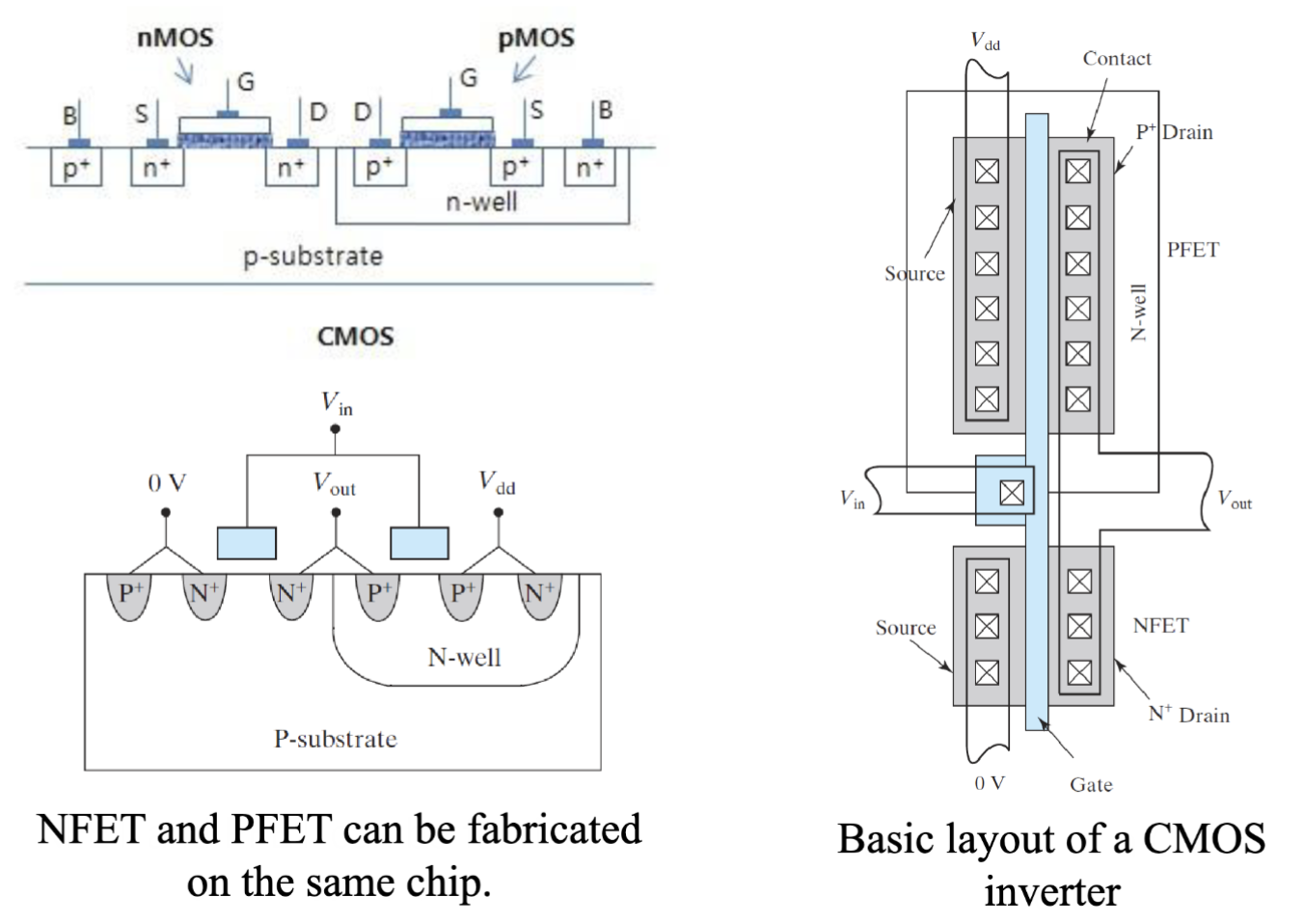
这两个 MOSFET 可以被直接制造在一个芯片上来实现高密度集成电路:
类似的,CMOS 还可以实现更多的逻辑电路功能,如
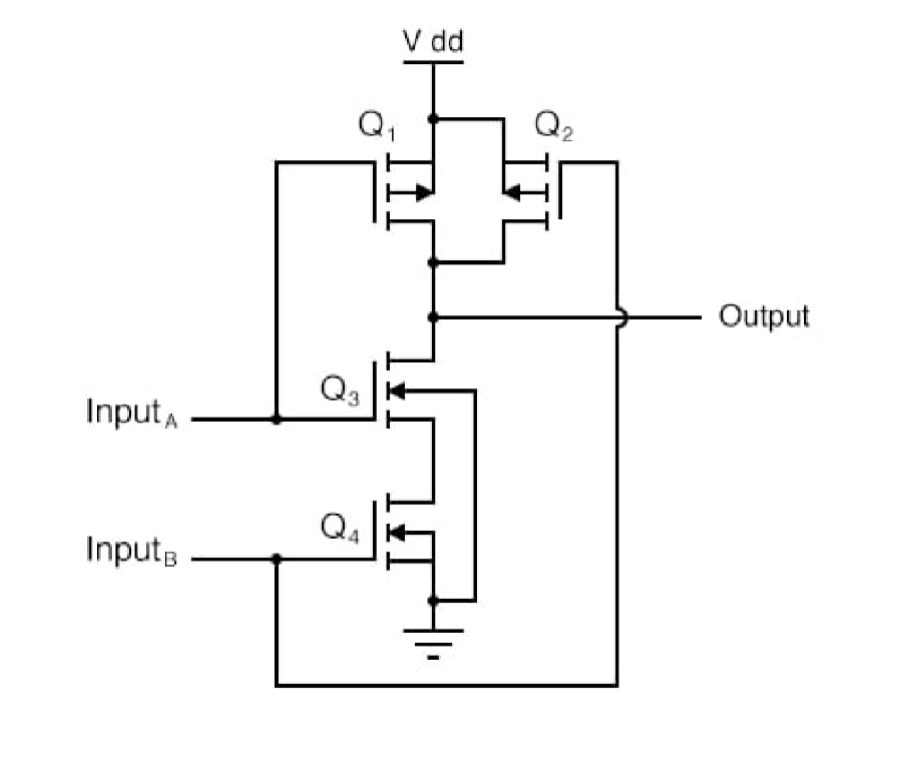
这个是一个是一个 CMOS 与非门 (NAND Gate) 的电路图。当输入 A 和 B 都为高电平时,NMOS 导通,PMOS 截止,输出被拉到低电平;在其他情况下,PMOS 导通,NMOS 截止,输出被拉到高电平。
然后,因为 NAND 是一个最小完全集,所以可以通过组合 NAND 门来实现任意逻辑函数。这使得 CMOS 技术成为现代数字电路设计的基础,广泛应用于微处理器、存储器和各种数字系统中。
Block.4 高级半导体器件
光电二极管 (Photodiodes)
背景知识
光电子 (Optoelectronic) 指的是半导体有和光子相互作用的功能。对应的,光电子器件 (Optoelectronic Devices) 则是可以检测或者发射光子的器件。
光电导体 (Photoconductors) 指的是表现出光电特性的器件或者材料,这种材料在光照下电导率发生变化。
光电子器件有非常多的种类,包括将光能转换成电能的器件以及光子的发射器。对于前者,典型的有光电二极管 (Photodiodes) 和太阳能电池 (Solar Cells);对于后者,典型的有发光二极管 (LEDs) 和激光形式存在的相干光源,也就是激光 (Lasers)。
光电二极管原理
产生电子-空穴对
光电二极管是一种设计用来响应光子吸收的二端口半导体器件。有些光电二极管有着极高的灵敏度和响应速度,由于现代的电子学通常同时涉及光信号和电信号,光电二极管作为光电转换器件在很多应用中都非常重要,比如光纤通信系统、光学传感器、光学测量仪器等。
长这个样子:
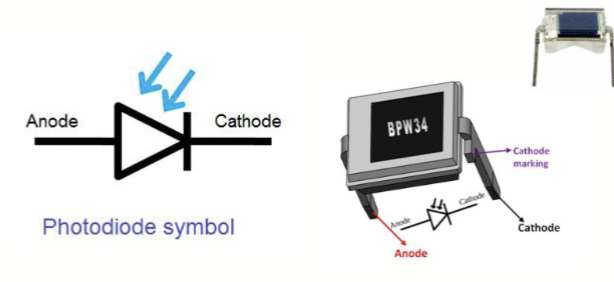
在没有外加偏置电压的情况下,二极管内部的能带图是这样的:
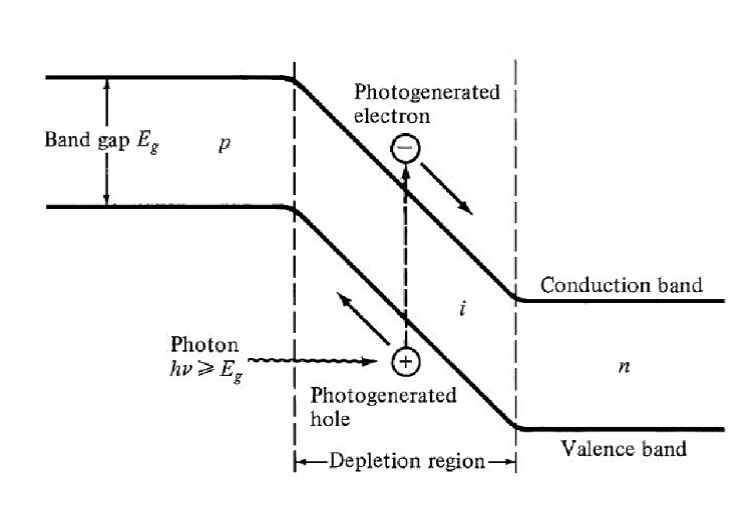
因为 P 型半导体和 N 型半导体中的能级差异,光电二极管有内建电势。
当来自入射光的光子击中光电二极管,他们可能会被吸收。如果光子的能量大于半导体材料的带隙能量,半导体中就会被激发出一个电子-空穴对。电子会移动到 N 型区域,而空穴会移动到 P 型区域。这种载流子的分离是由于内建电场的作用。
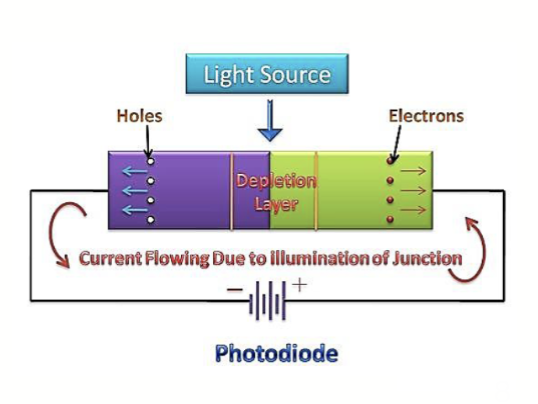
如果给光电二极管施加反向的外部电压作为偏置,二极管中的耗尽区的宽度会增加,从而增强了内建电场的强度。这种增强的电场有助于更有效地分离和收集由光子产生的电子-空穴对,减少了载流子的复合几率,提高了光电二极管的响应速度和灵敏度。
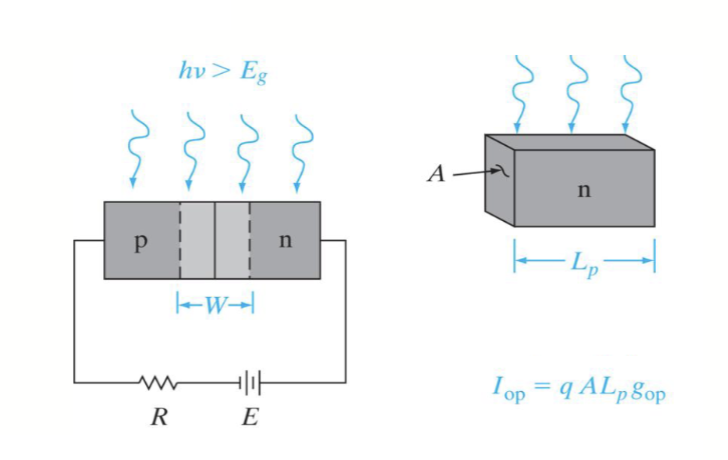
光子激发产生的电子和空穴产生的电流被称为光电流 (Photocurrent)。光电流的大小与入射光的强度成正比,因此光电二极管可以用来测量光强。
其中, 是电子的电荷量, 是二极管的横截面积, 是光生载流子产生率, 和 分别是 P 型和 N 型区域的少数载流子扩散长度, 是耗尽区的宽度。
光电二极管的 I-V 特性
如果把热生电流计算为 ,那么光电二极管的总电流可以表示为
其中, 是外加电压, 是玻尔兹曼常数, 是绝对温度。最后得到的值实际上是常规二极管方程描述的电流减去光电流。也就是说,在偏置恒定的情况下,不同的光照相当于把二极管的 I-V 曲线整体向下平移。
当二极管两端偏置大小为 0 时,器件短路,整个器件中只剩下的光电流。此时
当二极管两端开路时,通过器件的总电流大小为 0,带入原式子可得
其中, 称为开路电压 (Open-Circuit Voltage)。
光电二极管的工作状态
从我们之前的描述,不难看出,光电二极管一般工作在反向偏置状态下,基本是 I-V 曲线的第三第四象限部分。
在第三象限 (以及正向导通)的部分,主要是外部电路向光电二极管内部输送功率;在第四象限部分,光电二极管将吸收的光能转换为电能,向外部电路输送功率。
当光电二极管在被施加反向偏置,在第三象限工作时,电流大小因为二极管特性,与电压大小基本无关,而主要取决于入射光的强度。在这个状态下,光电二极管就相当于一个光控电流源。
在大部分光探测应用中,探测器的响应速度是至关重要的,对应的就是二极管中可以响应光照的部分:耗尽层宽度 。耗尽层宽度增大,响应速度也会增大,但是同时光子在半导体中的吸收率会降低,从而降低光电流的大小。因此,在设计光电二极管时需要在响应速度和灵敏度之间进行权衡。
控制耗尽层宽度的一种编写方法是使用 p-i-n 结构 (p-i-n Structure)。这种结构在 P 型和 N 型半导体之间插入一个本征半导体 (Intrinsic Semiconductor) 层。这样可以显著增加耗尽层的宽度,从而提高响应速度,同时保持较高的光子吸收率。
光电二极管的参数
这是原本的 PN 二极管结构,由一个 PN 结组成,在反向偏置下工作。
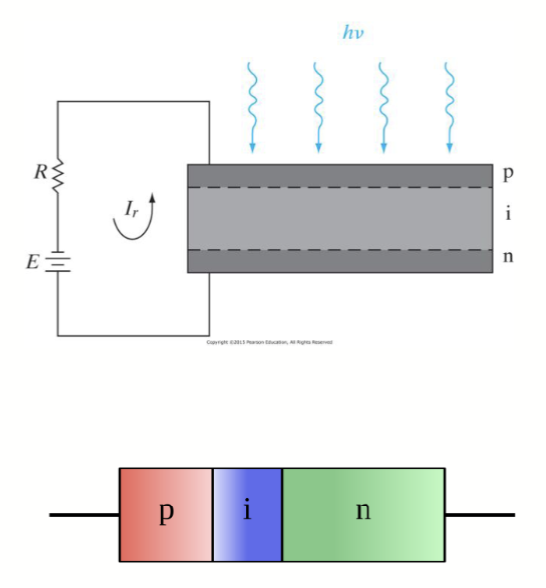
这是 PIN 结构下的光电二极管,在 P 和 N 类型中加了一个本征半导体层。其有很低的暗电流,也就是在没有光子进入二极管时,流过二极管的电流非常低。同时,其可以在更宽的波长范围内探测光。这让 PIN 结构的光电二极管被用作高速和低噪声的光探测器。
还有一种雪崩光电二极管 (Avalanche Photodiode, APD),其工作原理是利用高电场下的载流子碰撞电离效应来实现内部增益,从而提高光电流的强度。APD 通常在更高的反向偏置下工作,以产生足够的电场强度来引发雪崩效应。其被用于微光检测,如天文学、光纤通信和激光雷达等系统中。
控制光电二极管工作的主要方式时产生的光电流 ,入射光功率 和响应度 之间的关系。
在不同的波长下,响应度会有所不同。响应度还可以表示为
其中, 是量子效率 (Quantum Efficiency),表示每个入射光子产生的电子-空穴对的数量; 是普朗克常数, 是光子的频率, 是光子的波长,单位为微米。
常见材质下的光电二极管响应度曲线如下:
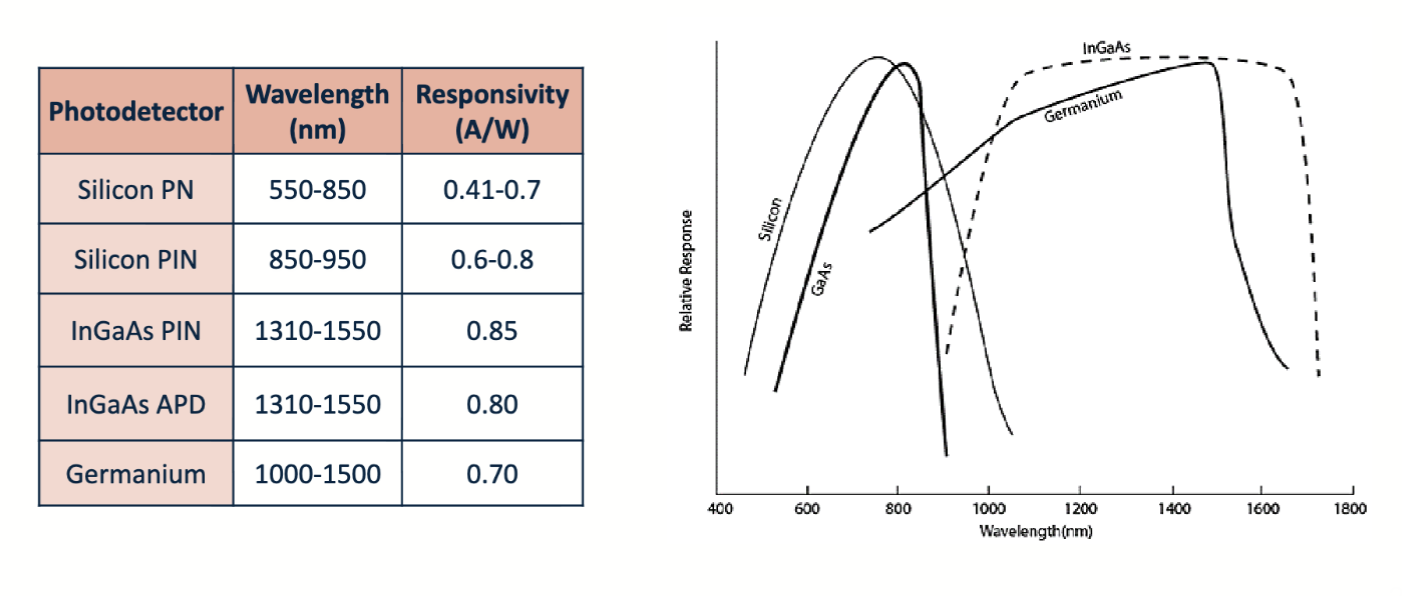
在反向偏置区中,即使没有入射光,光电二极管中也会有少量电流流过,这个电流被称为暗电流 (Dark Current)。暗电流主要来源于热激发产生的载流子,这些载流子在没有光照的情况下也能在半导体中移动。随着方向偏置的增大,暗电流会略微增大,受材料、温度、有效区域面积等因素影响。
通常硅基器件比锗基器件有更低的暗电流。
光电二极管的工作区域
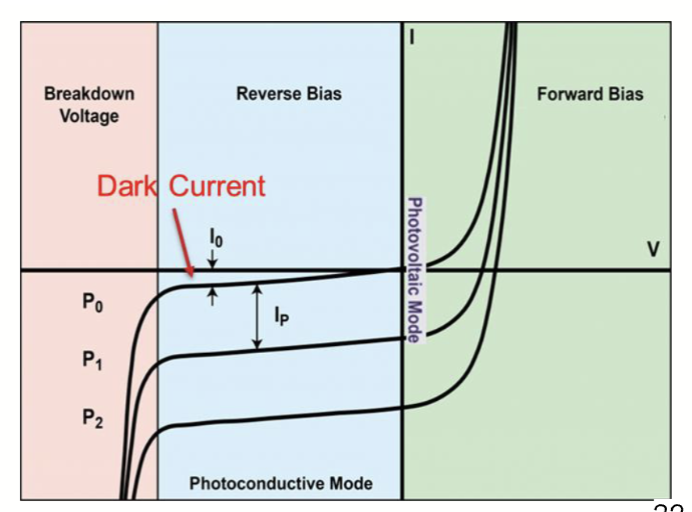
光电二极管一共有两种不同的工作方式,不同的工作模式选择主要取决于应用的速度要求和可容忍的漏电流大小。
在光电导模式 (Photoconductive Mode) 下,光电二极管被施加反向偏置电压。这样可以增加耗尽区的宽度,提高响应速度和线性度。光电导模式适用于需要快速响应和高线性度的应用,如高速光通信和精密光测量。
其通常有较大的暗电流,但是可以通过材料加以限制。
对应的,没有外加偏置电压的工作模式被称为光伏模式 (Photovoltaic Mode)。在这种模式下,光电二极管工作在零偏置状态,主要用于太阳能电池等应用。光伏模式下,光电二极管产生的电压和电流直接由入射光决定,适用于低功耗和环境光检测等场景。
这种模式有最小的暗电流,但是响应速度较慢。这个模式同时也是太阳能电池的工作模式。
发光二极管 (LED)
发光二极管概述
发光二极管本质上是一个 PN 结,由直接带隙半导体材料 (direct bandgap semiconductor) 制成,比如 GaAs。其中的电子和空穴复合会发射光子,从而实现电能到光能的转换。发射出来的光子能量近似等于半导体的带隙能量:
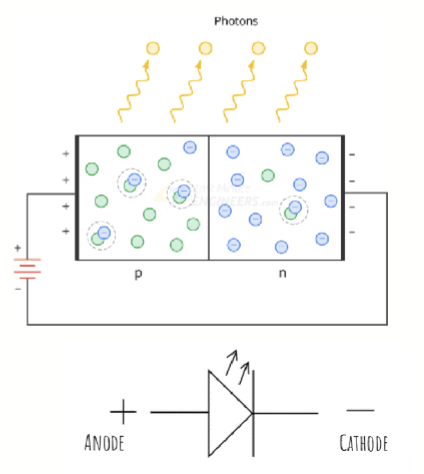
直接带隙指的是导带和价带的能量极值点在动量空间 (momentum space) 上重合,这使得电子从导带到价带的跃迁更容易发生,并且能够高效地发射光子。相比之下,间接带隙半导体(如硅)由于需要声子的参与,导致光发射效率较低,因此不适合用于 LED。如下图
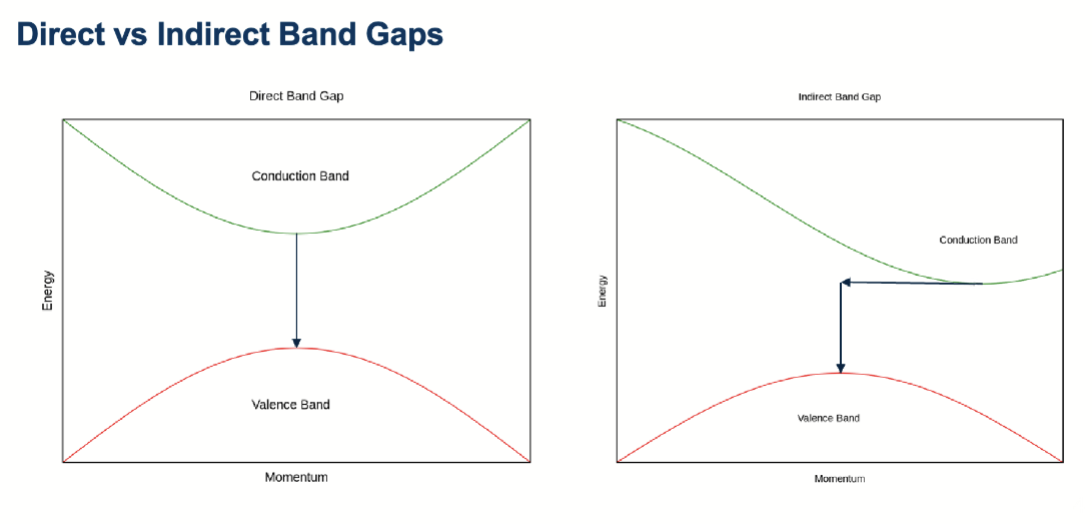
左图的导带和价带的极值点在横坐标上是对齐的,表示直接带隙;右图中导带极值点和价带极值点在横坐标上不对齐,表示间接带隙,电子需要改变一定的动量才能完成跃迁。
LED 通常由半导体材料制成,比如 GaAs, GaN, InGaN 等,不同的半导体材料因为有不同的带隙能量,从而发射不同波长的光。通过调节材料的组成,可以实现从红外到紫外的不同颜色的 LED。
LED 被广泛运用,因为其高效性、多种色彩变化、长寿命、开关自由、有方向性、体积紧凑、环保、高可靠性等优点。
常见的 LED 可以分为
- 标准 LED : 在可见光内发光,有多种颜色,用于普通照明和消费电子等
- IR LED : 发射红外光,常用于遥控器、夜视设备和光通信等应用。
- 大功率 LED : 用于高亮度照明且集中照明,如汽车大灯、建筑照明、手电筒、舞台照明、高强度应用场景
- RGB LED : 由红、绿、蓝三种颜色的 LED 组成,可以通过调节三种颜色的亮度来实现多种颜色的显示,常用于显示屏、氛围照明、变色照明、娱乐和装饰等
LED 的工作原理
传统的 LED 结构有这个几个部分:
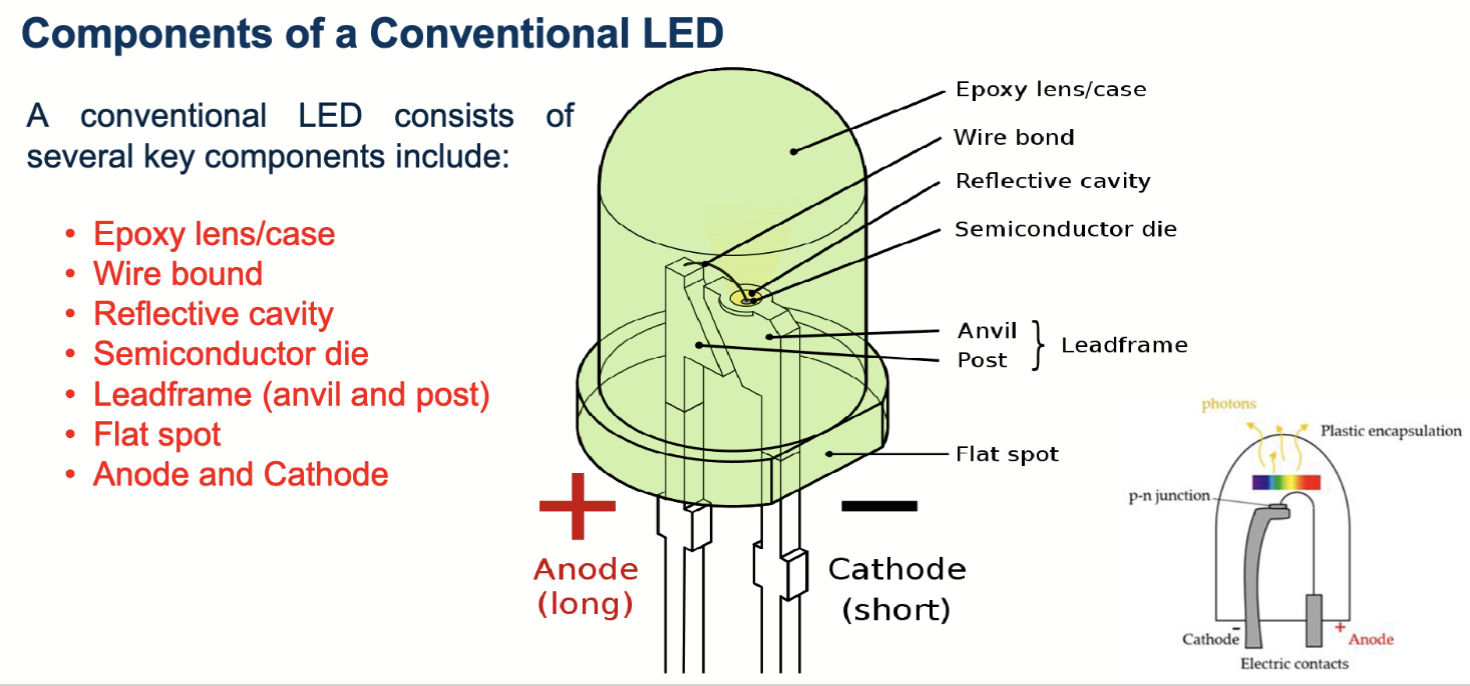
- 环氧树脂 (Epoxy) 的外壳
- 缝合引线
- 反射腔
- 半导体裸片
- 引线框架
- 平面点
- 阴极和阳极
其结构简单来说,是将裸片封装在一个透明的环氧树脂中,环氧树脂起到保护和光学透射的作用。引线框架和缝合引线用于将 LED 连接到外部电路。反射腔用于提高光的提取效率,将更多的光导向外部。
LED 中的能带图如下:
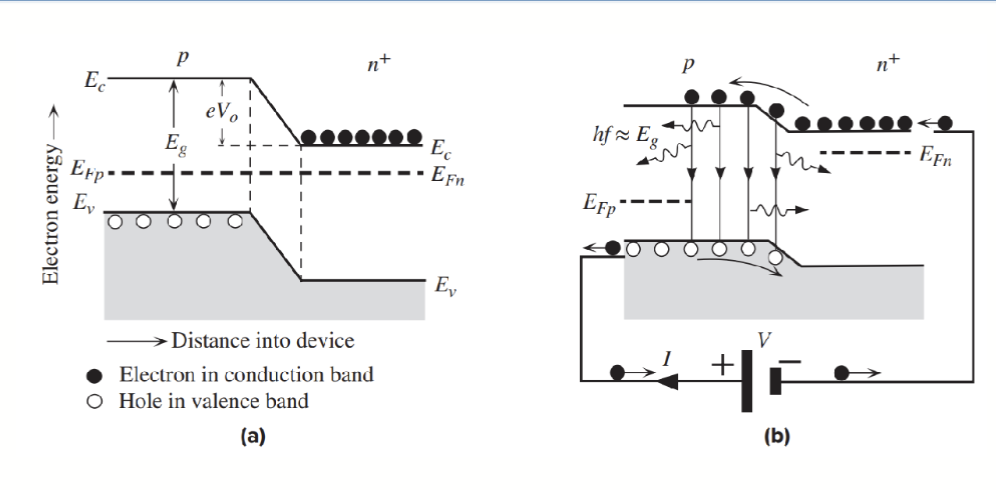
左图是没有外加偏置的情况,n 型半导体是重掺杂的,p 层通常很薄,整个器件的费米能级是统一的,也就是
当是加了一个正向偏置 时,PN 结附近以及 P 区的电子扩散长度内的电子直接复合,导致光子发射。左右两侧的费米能级分离,。
这种发光过程叫做电致发光 (Electroluminescence, EL),指的是电流通过材料时,由于空穴和电子的辐射复合 (radiative recombination) 而产生光的现象。对于重掺杂 N 型的 PN 结中,由于少数载流子输入导致电子-空穴对复合而发光的现象被称为注入型电致发光 (Injection Electroluminescence)。
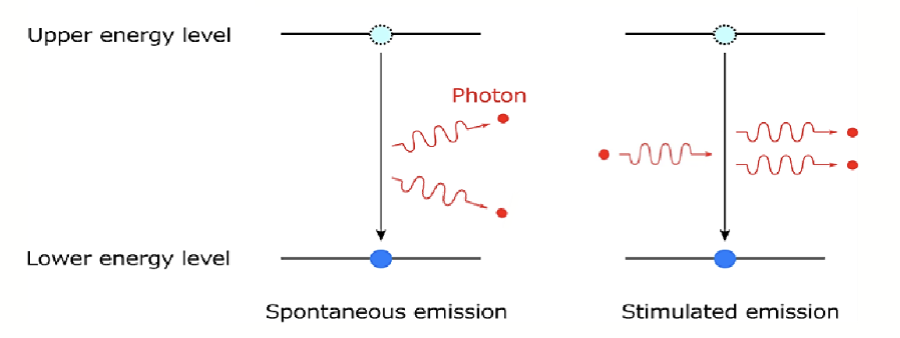
由于电子和空穴之间复合过程的统计性质, LED 发射的光子方向是随机的,他们源于电子和空穴之间的自发辐射复合 (Spontaneous Radiative Recombination),这种自发复合过程导致了自发光子发射 (Spontaneous Photon Emission)。
LED 发射的光是非相干光 (Incoherent Light),与激光器发射的相干光不同。
不同 LED 的结类型
LED 可以有不同的结类型,主要有以下几种:
- 同质结 (Homojunction) :有两种不同掺杂方式但是相同材料的 PN 结,比如 GaAs 的 P 型和 N 型区域组成的 LED。
- 异质结 (Heterojunction) :由不同材料组成的 PN 结,比如 GaAs 和 AlGaAs 组成的 LED。异质结可以提供更好的载流子注入效率和光子提取效率。
- 双异质结 (Double-Heterojunction, DH) :在 P 型和 N 型区域之间插入一个不同材料的本征半导体层 (Intrinsic Layer),形成 P-I-N 结构。这样可以更有效地限制载流子扩散,提高发光效率。
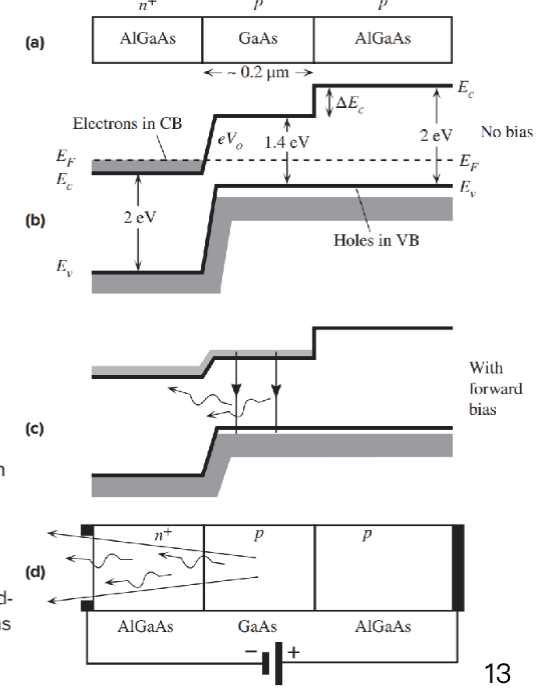
量子阱高亮度 LED
常见的量子阱(Quantum Well, QW) 结构如下:
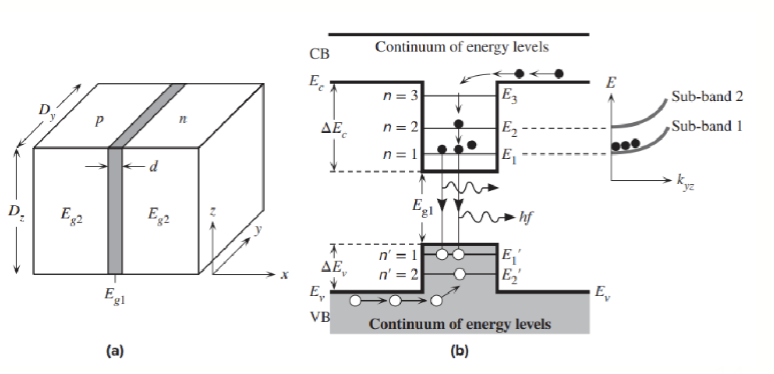
其中间包含一个超薄的窄带隙半导体,带隙大小为 ,两侧是宽带隙半导体,带隙大小为 。这一层被称为限制层 (Confining Layer),其作用是将电子和空穴限制在量子阱中,从而提高载流子浓度和复合效率。比如两边的半导体材料是 AlGaAs,中间的量子阱部分是一个薄的 GaAs 层。
这两种半导体是晶格匹配的 (Lattice-matched),这样可以减少界面缺陷,提高器件性能。通过调整量子阱的厚度和成分,工程师可以控制能级 ,进而控制发射光的波长。这对生产特定颜色的 LED 非常重要。
应用场景很广泛,比如显示、固态照明、医学成像、传感器、光通信、军事、娱乐
LED 的发光材料
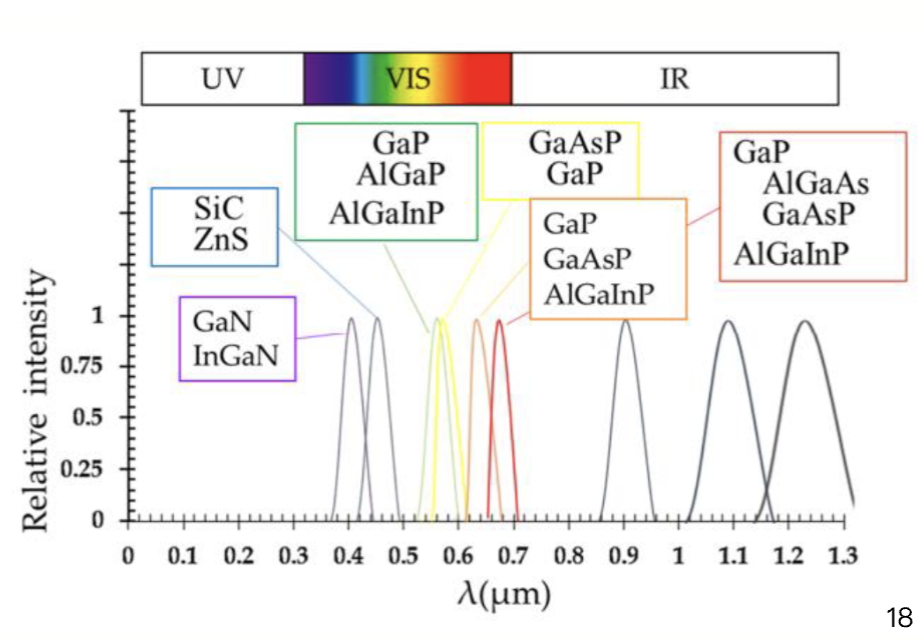
由于需要可见光和红外波长的半导体激光器和 LED,可用的 II-V 族的材料种类繁多,包括:
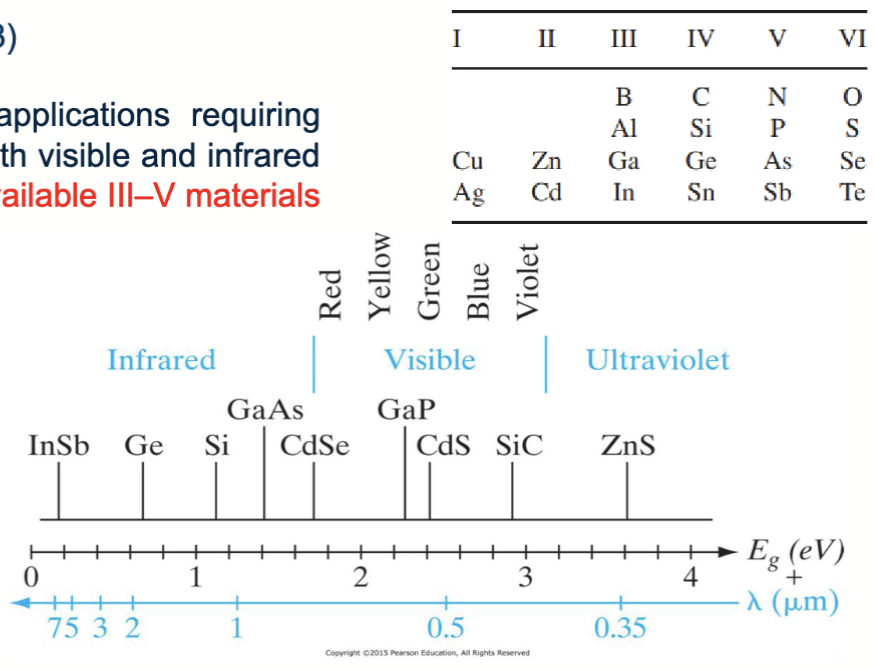
因为不同的材料的带隙差异很大,可以获得的光子能量范围也很广,从紫外光 (ZnS 3.6eV) 延伸到红外光 (InSb 0.18eV)
可见光的波长范围是
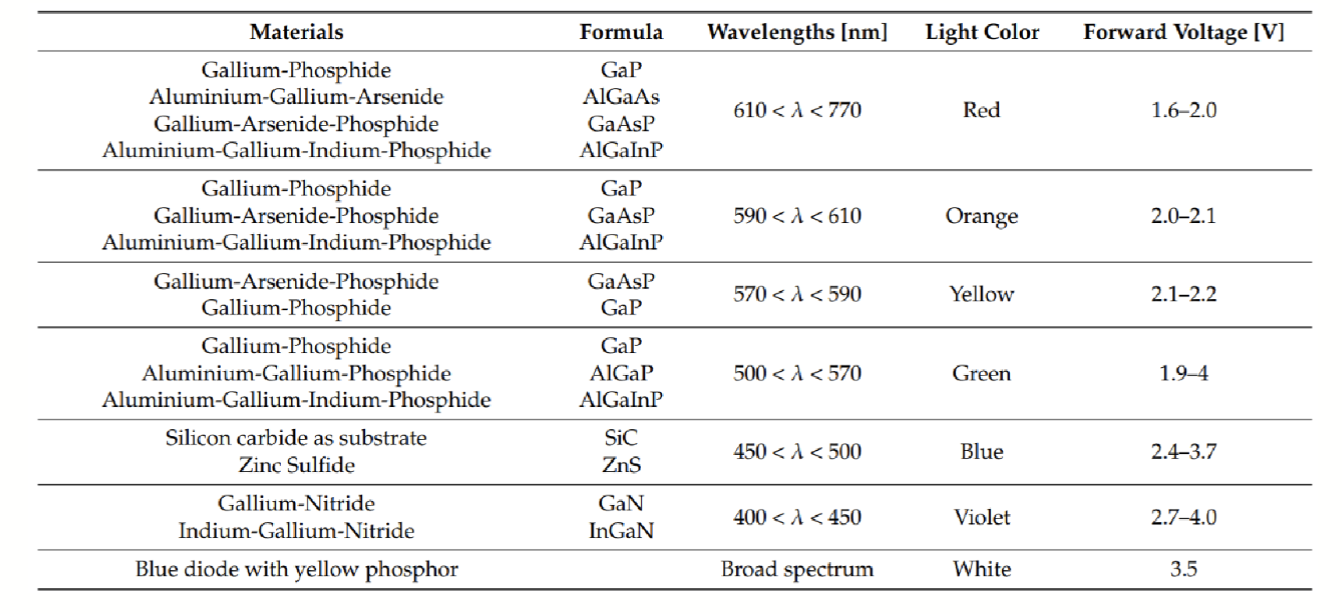
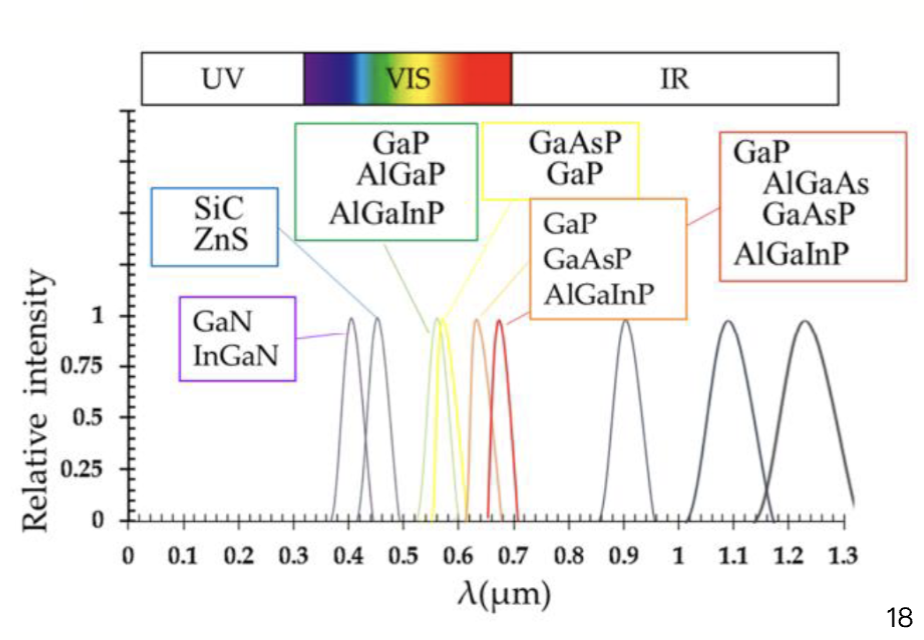
同时,不同半导体材料制成的 LED 发出的光的光谱分布也是不一样的。随着发射能量从光谱的红外端转移到紫外端,发射光谱在波长上变得更窄。
LED 的发光强度也在随着时间和工艺改进逐渐提高:
LED 的电学特性
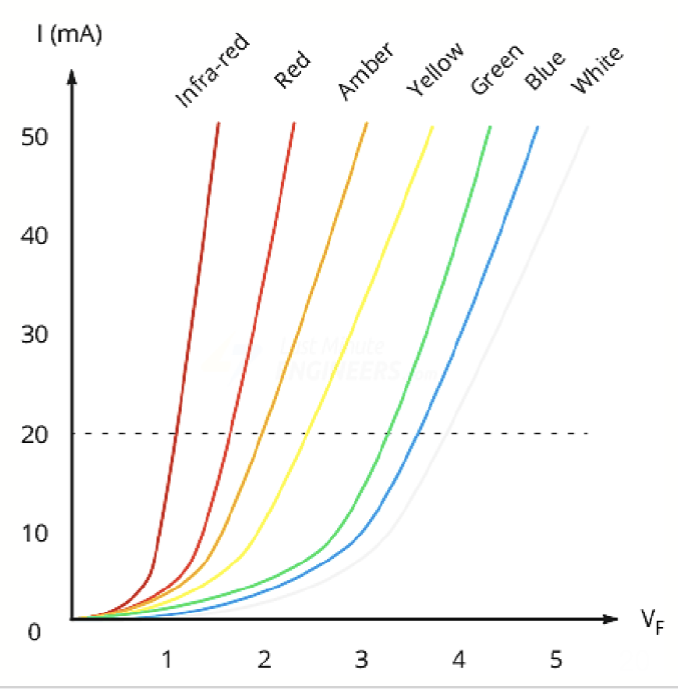
为了得到可见光,带隙大小应该大于 1.8eV。常见的 LED 的工作电压大约在 之间,额定电流大小大概为 到 ,其中最常见的范围是 。
如果跃迁发生在了直接带隙半导体中,发出的光子波长大小是:
和光电二极管类隙,LED 也有一个外量子效率 (external quantum efficiency, EQE),表示每个注入的电子-空穴对产生的光子数量。其定义为:
这里的 是内量子效率 (internal quantum efficiency),表示在半导体内部每个注入的电子-空穴对产生的光子数量; 是提取效率 (extraction efficiency),表示从半导体内部发射出来的光子中,有多少比例能够成功逃逸到外部环境中。
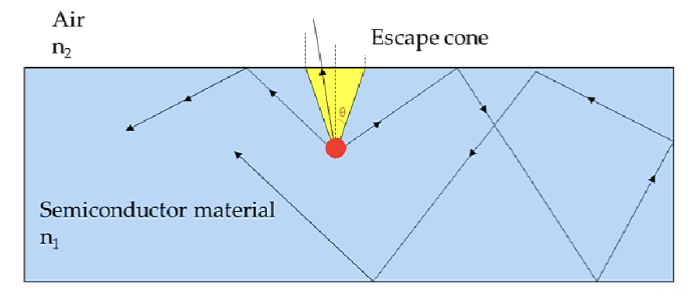
由于一开始产生的光子是在材料内部产生并且向随机方向发射的,因此,其在脱离材料时会发生全反射现象,能逃脱出去的范围我们称之为光逃逸锥 (Light Escape Cone)。其与内全发射 (Total Internal Reflection, TIR) 的角度有关。
这里的 是半导体材料的折射率, 是外部环境(通常是空气)的折射率。由于大部分半导体材料的折射率远大于空气,因此光逃逸锥的角度通常很小,导致提取效率较低。 被称为临界角 (critical angle)。
计算临界角对应的锥体对应的球冠形曲面面积:
然后整个球形的面积大小是 ,因此提取效率可以表示为:
可以看出,只有很小一部分光子能够成功逃逸到外部环境中。而对于大部分半导体材料,折射率相当高,比如 GaAs 的折射率大约是 3.5,那么临界角大约是 ,对应的提取效率大约只有 。
为了提高发光效率,一种常用的技术是使用透明塑料进行封装,这种塑料的折射率大概是 。这样可以增加临界角,从而提高提取效率。
太阳能电池 (Solar Cell)
太阳能电池简介
太阳能电池大多数使用使用的是硅材料,因为硅目前工艺成熟,可以以较低成本制造。现在的多晶硅电池的效率大概是 左右,单晶硅电池的效率大概是 左右。
在同一个警惕内制造 PN 结制成的太阳能电池被叫做同质结太阳能电池 (Homojunction Solar Cell),而使用不同材料制造 PN 结制成的太阳能电池被叫做异质结太阳能电池 (Heterojunction Solar Cell)。
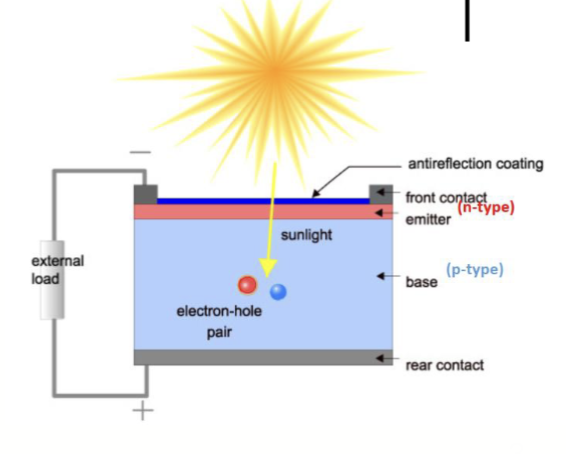
典型的结构如下图所示:
电路符号长这样:
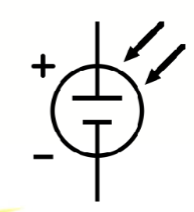
其原理在 1839 年被发现,在 1954 年被贝尔实验室 (Bell Labs) 制造出第一个实用的硅太阳能电池。
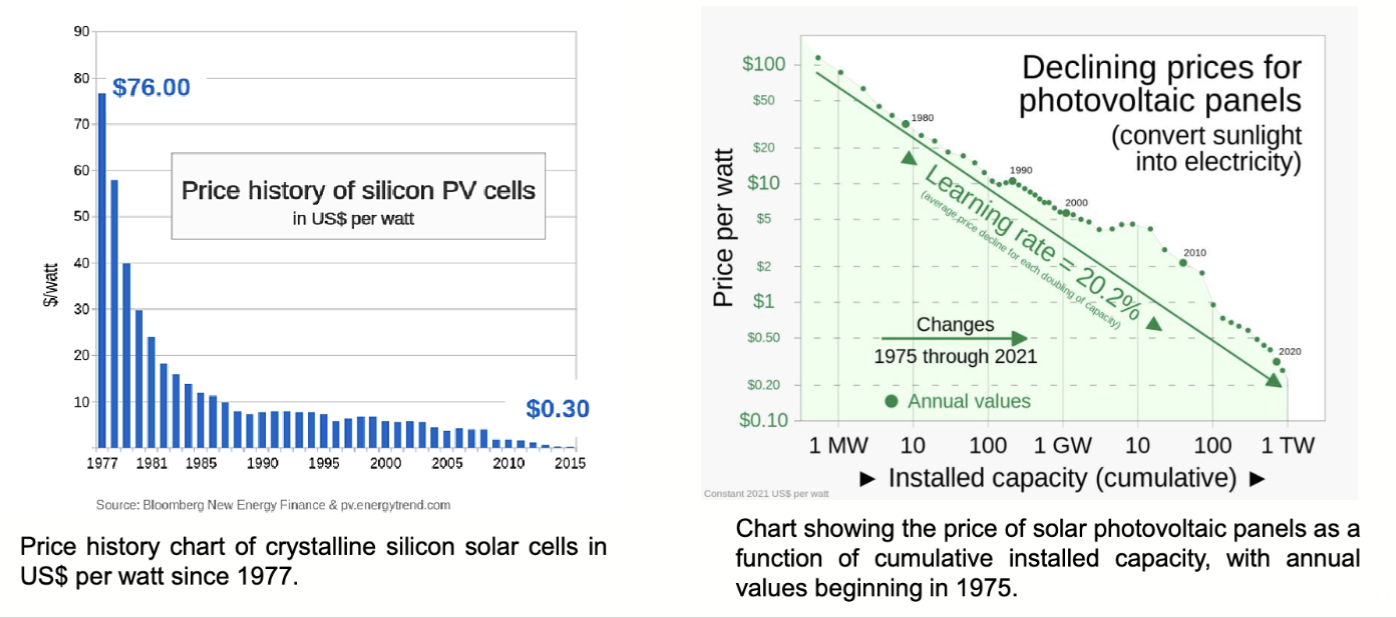
在 1977 年以来,太阳能电池随着时代变化和累计装机总量的增长,价格大幅下降,如下图所示。这也对 CO2 减排起到了重要作用。
太阳能电池的工作原理
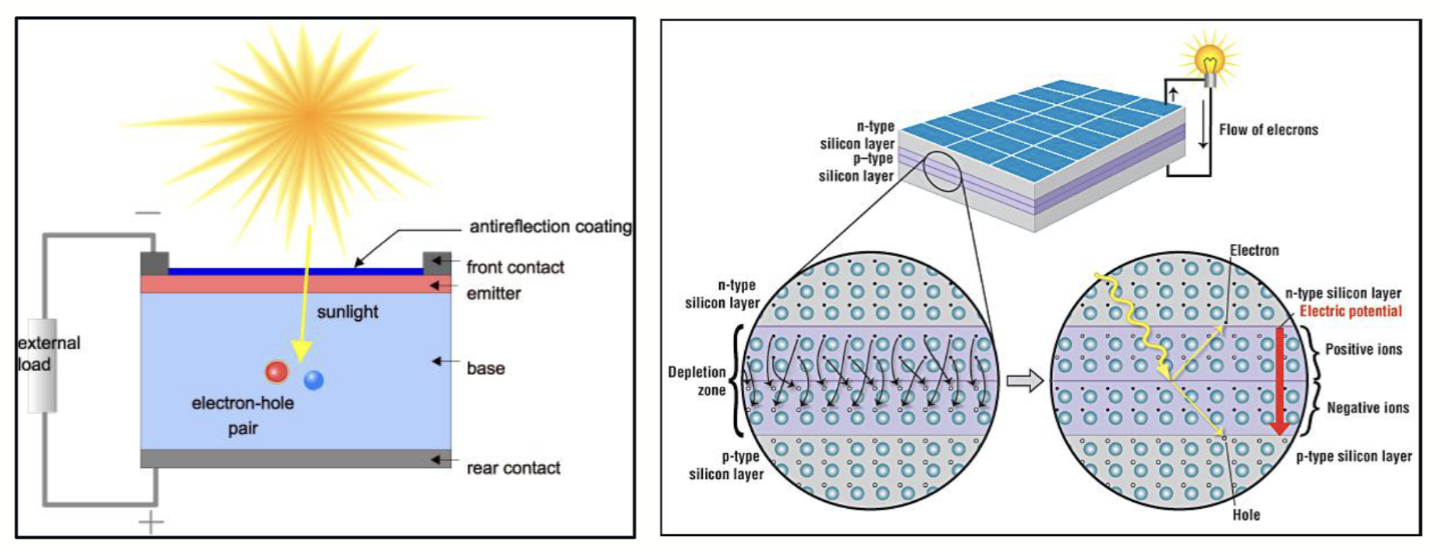
在光电二极管部分我们已经介绍过光生载流子的产生过程。太阳能电池的工作原理和光电二极管类似,都是利用 PN 结的内建电场将光生载流子分离,从而产生电流。
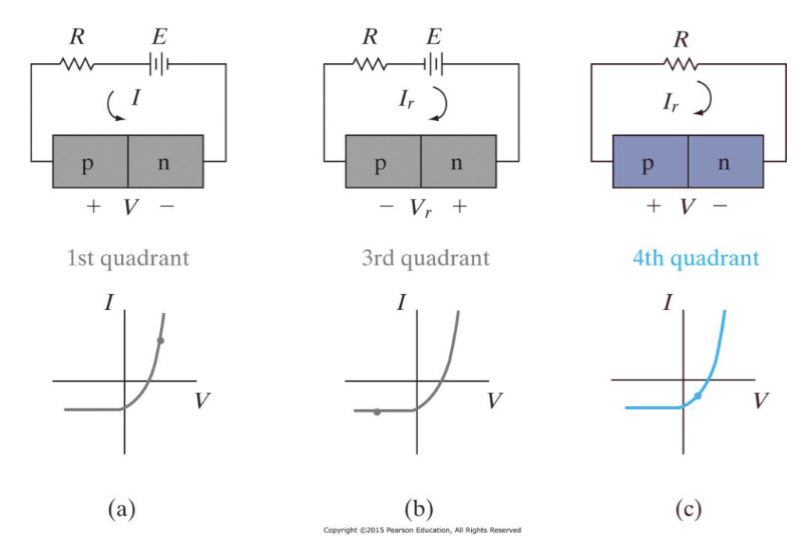
太阳能电池工作在光电二极管的第四象限部分,如下图所示。此时它才会对外提供电流和电压,从而输出功率。
而对于一个典型的太阳能电池,其简化图如图所示
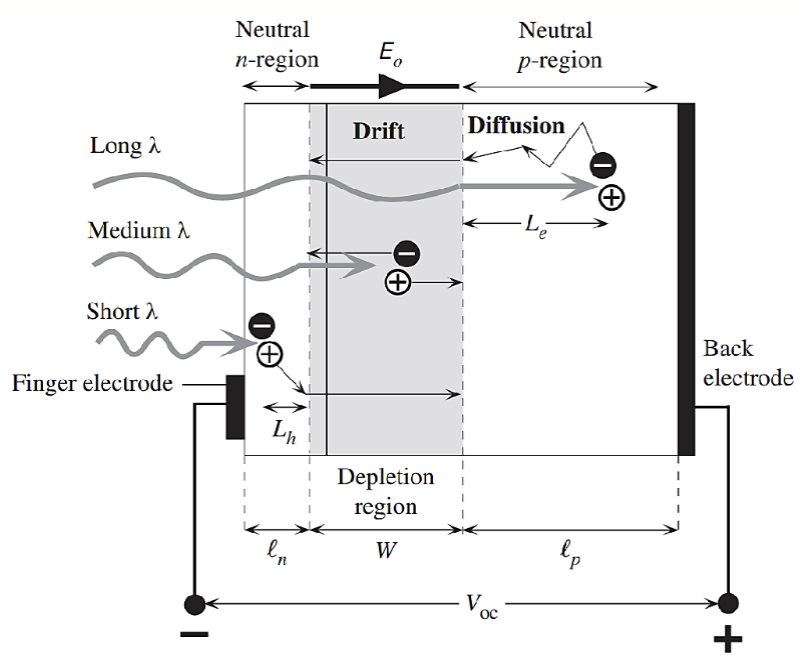
这是一个二极管,由一个 PN 结,其中 P 区非常窄,掺杂更重;P 区较宽,掺杂较轻。耗尽区主要向着 P 区一侧延伸。耗尽区中形成内建电场,随着光照变化。
光照射到电池比较薄的 N 区,产生电子-空穴对。由于内建电场的作用,电子被扫到 N 区,空穴被扫到 P 区,从而形成电流。
常见的二极管的电极是链接在 N 和 P 区的,但是太阳能电池的 N 区需要允许光照进入,同时需要较小的电阻以减小损耗,因此太阳能电池的 N 区电极通常是一个树枝状的金属网格,如下图所示:
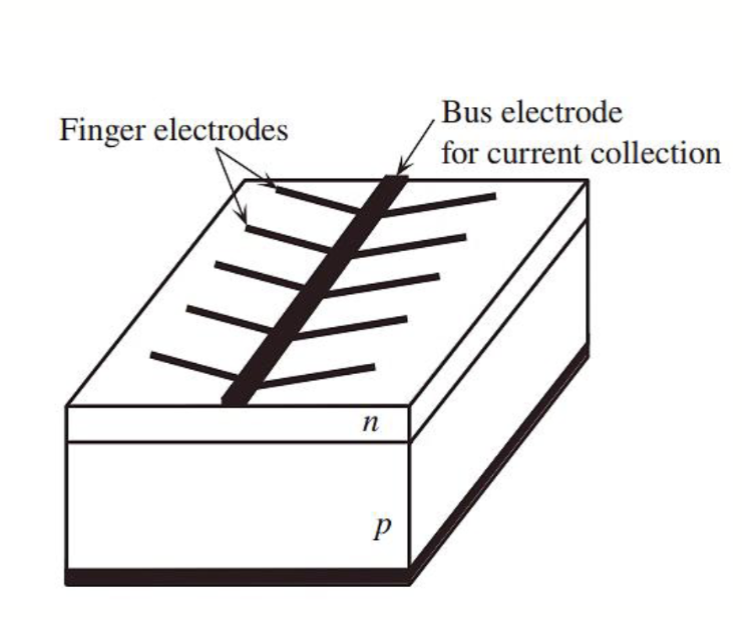
其有一个主干,连接到外部电路,其余的枝杈则尽可能在不挡住光照的情况下覆盖更多的面积以减小电阻损耗。
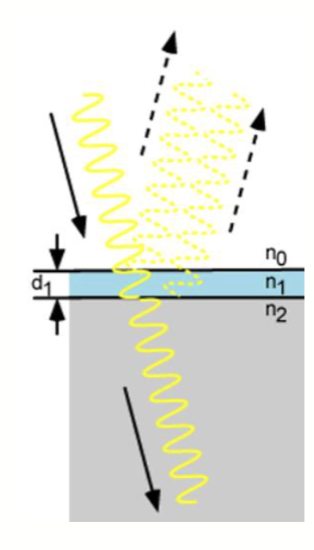
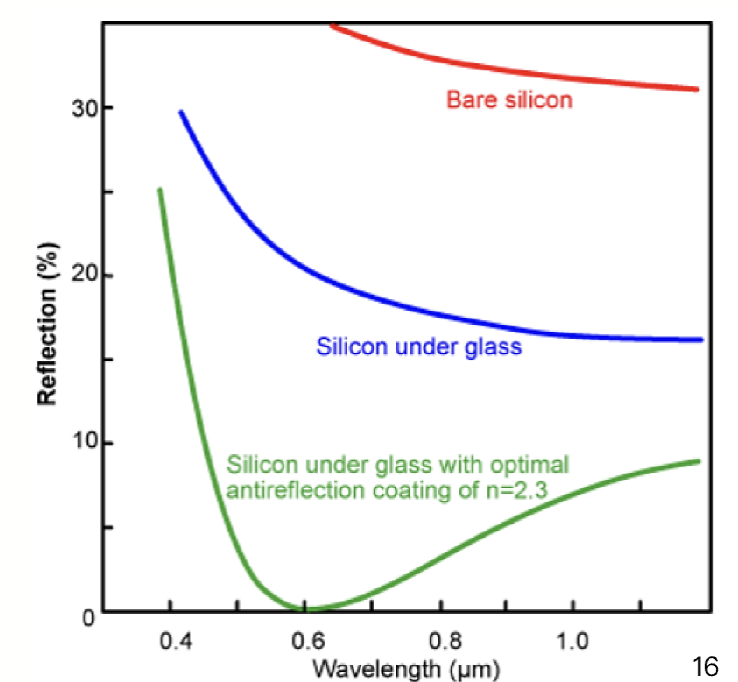
在太阳能电池上也会有一层抗反射层 (Anti-Reflection Coating, ARC),以减小光的反射损失,提高光的吸收效率。反射率的计算公式如下:
这里的 是空气的折射率, 是抗反射层的折射率, 是硅的折射率, 是抗反射层的厚度, 是入射光的波长。
最终的反射率与厚度、折射率、波长有关。因此,增透层的零反射特性只能在特定波长下发生。对于光伏应用,通常选择最小化 处的反射率,因为这是太阳光谱中最强的部分。
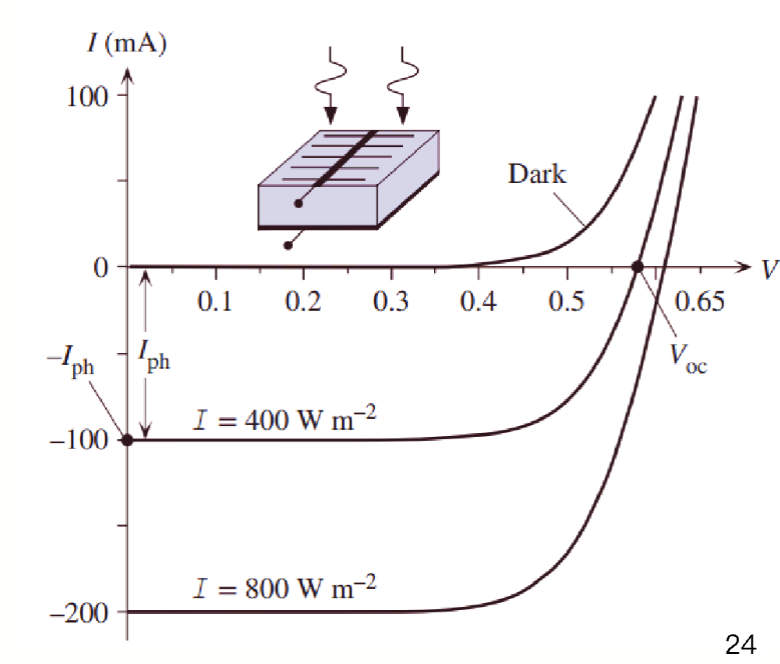
和在光电二极管那一张提到的一样,在光照条件下,产生的短路电流大小为
其中, 是电池面积, 是光生载流子产生率, 和 分别是电子和空穴的扩散长度, 是耗尽区宽度。
开路电压大小为
其中, 是暗态下的反向饱和电流。
太阳能电池阵列
单个太阳能电池无法提供很多功率,单个电池开路电压通常在 左右,产生的电流取决于面积,对于 面积的电池,电流大小 大概在 左右。因此,实际应用中通常将多个太阳能电池串联或并联组成太阳能电池阵列 (Solar Cell Array)。
太阳能组成的较大阵列被称为光伏组件 (Photovoltaic module),其中每个组件是由封装在环境保护层压板重点光伏电池组成的。
光伏面板 (Photovoltaic panel) 由多个光伏组件组成,通常用于屋顶或地面安装以收集太阳能。这些组件被组装成一个预先接线、可现场安装的单元。
光伏阵列是完整的发电单元,通常由多个光伏面板组成。

太阳能电池的伏安特性
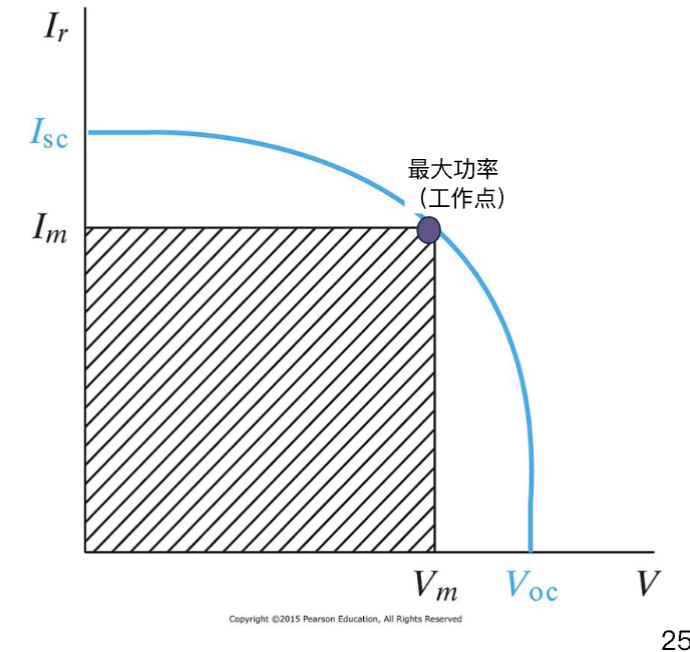
硅太阳能电池的伏安特性如图所示,短路电流表示为 ,开路电压表示为 。如果想要最大化一个太阳能电池的输出功率,就需要得到最大的 ,其中 和 分别是最大功率点 (Maximum Power Point, MPP) 处的电压和电流。
我们基于这个定义填充因子 (Fill Factor, FF) 来衡量太阳能电池的性能。这个参数表明了在最佳条件下,太阳能电池能多有效的将可用太阳光部分转化成电能。
填充因子是太阳能电池的一个品质因数,其值通常在 之间,越高表示太阳能电池的性能越好。标准硅光伏电池的填充因子大概是 。
不同种类的太阳能电池
常见的太阳能电池主要分为三类:单晶硅、多晶硅和薄膜太阳能电池。
单晶硅太阳能电池由单晶结构制成,通常使用高纯度的硅,以高效率和节省空间为特点。其制造过程复杂且成本较高,但效率通常在 以上。
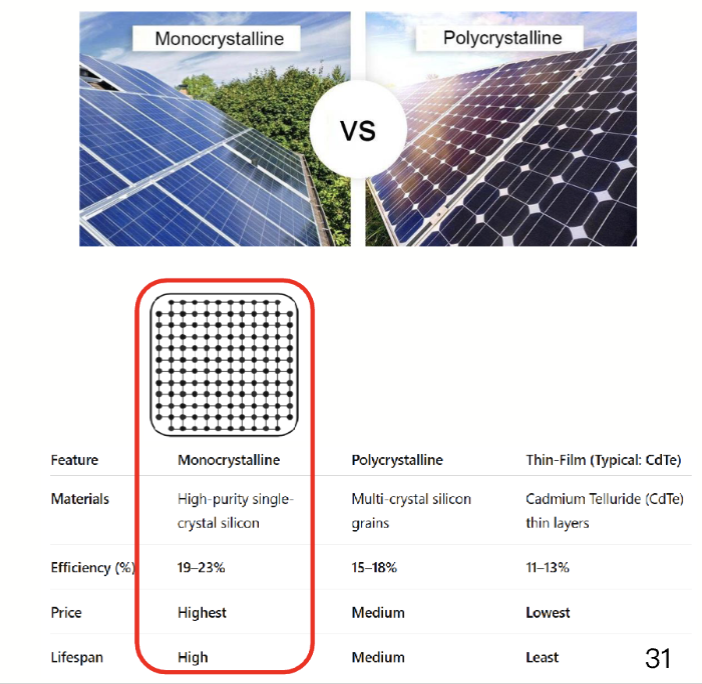
多晶硅太阳能电池使用多晶硅材料制成,通常形态不如单晶硅均匀;成本较低,效率较低,在成本和性能之间取得平衡。其效率通常在 到 之间。

薄膜太阳能电池是使用半导体材料薄层制造的,比如非晶硅 (a-Si)、碲化镉 (CdTe) 和铜铟镓硒 (CIGS) 等。其制造成本低,重量轻,灵活性好,但效率较低,通常在 到 之间。灵活,轻量化,便携,可以适用于各种表面。其在某些情况下有成本效益和优势