Lec.2.2 P-N Junction Part.2

PN 结的结电容

回顾一下 Lec.2.1 中提到的 PN 结相关的几个公式：

$$V_{bi}=V_T\ln \frac{N_A{N}_D}{n_i^2}=\frac{kT}{q}\ln \frac{N_A{N}_D}{n_i^2}$$

$$W=\sqrt{\frac{2{\epsilon }_0{\epsilon }_r(V_{bi}-V)}{q}(\frac{1}{N_A}+\frac{1}{N_D})}$$

$$I=I_0(e^{\frac{qV}{kT}}-1)$$

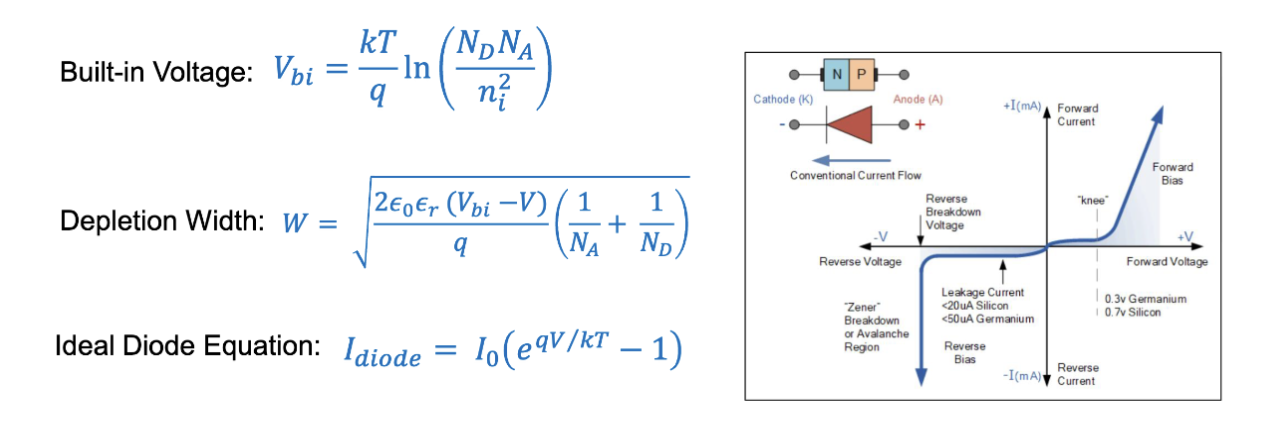
在耗尽层的两侧，电荷相互间隔，形成了一个电容器，其电容值可以通过以下公式计算：

$$C=\frac{ϵA}{W}=A\sqrt{\frac{qϵ}{2(V_{bi}-V)}(\frac{N_D{N}_A}{N_D+N_A})}$$

• $C$: PN 结的结电容 (Junction Capacitance)
• $ϵ={\epsilon }_0{\epsilon }_r$: 半导体的介电常数 (Permittivity of the Semiconductor)
• $A$: PN 结的面积 (Area of the PN Junction)
• 其他符号同上

在 PN 结中有 $N_A>>N_D$，所以可以简化为：

$$C=A\sqrt{\frac{qϵ}{2(V_{bi}-V)}{N}_D}$$

因此，测量二极管中的电容大小是一种间接测量掺杂浓度 $N_D$ 的方法。

载流子在电场作用下的运动

在半导体内部，载流子的行为主要分为两种

• 漂移 (Drift)
  • 载流子在电场作用下的运动
  • 例如，在 PN 结的耗尽区内，电场会使电子向 N 区移动，空穴向 P 区移动
• 扩散 (Diffusion)
  • 载流子由于浓度梯度而发生的运动
  • 例如，在 PN 结的两侧，载流子会从高浓度区域扩散到低浓度区域

漂移

在施加了外部电场 $E$ 的情况下，电场力会对载流子施加作用力。这个力叠加在电子的随机作用上，可以看作粒子以一个恒定的平均漂移速度运动

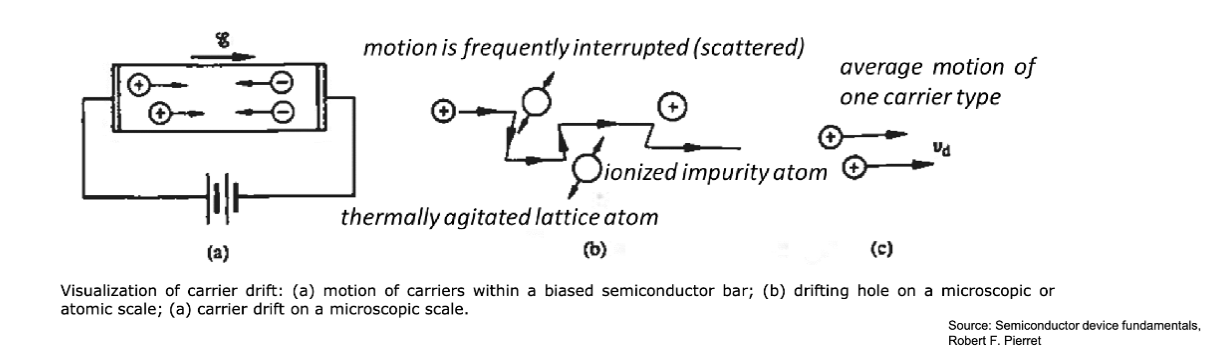
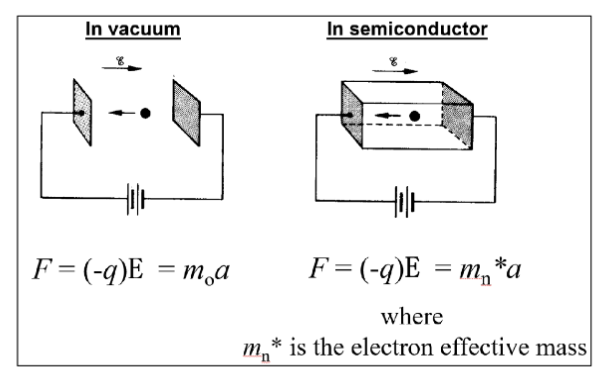
施加在粒子上的力的大小为 $F=qE$，引起的加速度大小是 $a=\frac{F}{m}$ 。电场的加速作用同时由粒子的质量和电荷决定，也就是质荷比。在半导体中，质量用 $m^{\ast }$ 表示，称为 有效质量 (Effective Mass)。其由半导体的能带结构决定。

漂移速度 (Drift Velocity) 指的是当施加电场时材料中载流子的速度。在低电场下有公式:

$$v=\mu E$$

其中， $\mu$ 是载流子的迁移率 (Mobility)，表示载流子在电场作用下的响应能力。迁移率的单位是 $c{m}^2/Vs$。在半导体材料中，电子和空穴的迁移率 ${\mu }_e$ 和 ${\mu }_h$ 通常不同，通常取决于温度、掺杂浓度和其他因素等。

漂移电流密度 (Drift Current Density) 指的是由于电场的影响，半导体中的载流子的运动引起的单位面积的电流的流动。对于电子和空穴，漂移电流密度可以表示为：

$$\begin{array}{rl}& J_n=qn{v}_D=qn{\mu }_{n}E\text{(电子的漂移电流密度)}\\ & J_p=qp{v}_D=qp{\mu }_{p}E\text{(空穴的漂移电流密度)}\end{array}$$

总的漂移电流密度为：

$$J_{drift}=J_n+J_p=q(n{\mu }_n+p{\mu }_p)E$$

扩散

扩散 (Diffusion) 指的是载流子的热运动引起的，从高浓度区域向低浓度区域的净移动过程。这种现象是由于载流子在材料中的随机热运动所导致的。在半导体中，扩散电流密度 (Diffusion Current Density, $J$ ) 可以用菲克定律 (Fick’s Law) 来描述：

$$\begin{array}{rl}& J_{n,\mathrm{diffusion}}=-q{D}_n\frac{dn}{dx}\text{(电子的扩散电流密度)}\\ & J_{p,\mathrm{diffusion}}=q{D}_p\frac{dp}{dx}\text{(空穴的扩散电流密度)}\end{array}$$

从公式可以看出，扩散电流大小取决于浓度梯度大小和相应的载流子的扩散系数。其中， $\frac{dn}{dx}$ 和 $\frac{dp}{dx}$ 分别表示电子和空穴浓度关于位置 $x$ 的变化率， $D_n$ 和 $D_p$ 分别是电子和空穴的扩散系数，单位是 $c{m}^2/s$ 。

扩散系数 (Diffusion Coefficient, $D_n$ 和 $D_p$ ) 描述了载流子在浓度梯度作用下在材料中扩散的难易程度。其与迁移率之间存在爱因斯坦关系 (Einstein Relation)：

$$\begin{array}{rl}& D_n={\mu }_n\frac{kT}{q}\text{(电子的扩散系数)}\\ & D_p={\mu }_p\frac{kT}{q}\text{(空穴的扩散系数)}\end{array}$$

两者都取决于载流子迁移率 ${\mu }_n$ 和 ${\mu }_p$ 以及温度 $T$ 。更高的迁移率会导致更高的扩散率。这种关系将载流子的热运动（也就是扩散）和其对电场的响应（也就是迁移）联系起来。

总载流子电流

半导体中的总载流子电流密度 (Total Carrier Current Density) 是漂移电流密度和扩散电流密度的总和。对于电子和空穴，净载流子电流密度可以表示为：

$$\begin{array}{rl}J& =J_n+J_p\\ & =J_{n,\mathrm{drift}}+J_{n,\mathrm{diffusion}}\\ & +J_{p,\mathrm{drift}}+J_{p,\mathrm{diffusion}}\end{array}$$

电导率和电阻率

电导率 (Conductivity, $\sigma$ ) 指的是电流密度 $J$ 与施加在材料上的电场大小 $E$ 之间的比例系数。半导体的总电导率的计算方式是：

$$\sigma =q(n{\mu }_n+p{\mu }_p)$$

其中， $n$ 和 $p$ 分别是材料中电子和空穴的浓度， ${\mu }_n$ 和 ${\mu }_p$ 分别是电子和空穴的迁移率。

对应的，电阻率 (Resistivity, $\rho$ ) 是电导率的倒数，它衡量得失材料对电流流动的阻碍程度。它受载流子数量以及其在材料中的移动难易程度，也就是迁移率的影响。电阻率的计算方式是：

$$\rho =\frac{1}{\sigma }=\frac{1}{q(n{\mu }_n+p{\mu }_p)}$$

但是，怎么确定电子浓度和空穴浓度？

过程涉及到态密度 (Density of States, $g_{\mathrm{cb}}(E)$ ) 和状态占据概率 (Occupation Probability, $f(E)$ )。最终的计算方式是将二者相乘并积分：

$$\begin{array}{rl}n& ={\int }_{E_c}^{E_c+x}{n}_E(E)dE\\ & ={\int }_{E_c}^{E_c+x}{g}_{\mathrm{cb}}(E)f(E)dE\end{array}$$

在此处， $E_c$ 是导带的底部能级， $x$ 是一个足够大的能量范围，确保包含了所有可能的电子态。通过这个积分，我们可以计算出在给定条件下材料中的电子浓度 $n$ 。

此处费米函数 (Fermi Function) $f(E)$ 描述了占据可用能级的概率:

$$f(E)=\frac{1}{\exp (\frac{E-E_F}{kT})+1}$$

其中， $E_F$ 是费米能级 (Fermi Level)，表示在绝对零度下电子填充到的最高能级。 $k$ 是玻尔兹曼常数， $T$ 是绝对温度。

而态密度的定义是可用能级的数量，进而决定有多少电子可以到达导带。其计算方式为:

$$g_{\mathrm{cb}}(E)=\frac{(\pi 8\sqrt{2})m_e^{\ast \frac{3}{2}}}{h^3}\sqrt{E-E_c}$$

其中， $m_e^{\ast }$ 是电子的有效质量， $h$ 是普朗克常数， $E_c$ 是导带的底部能级。

把这些定义带入上述的积分公式中，可以计算出材料中的电子浓度 $n$ 。类似地，可以通过类似的积分计算出空穴浓度 $p$ 。

$$\begin{array}{rl}n& \approx \frac{(\pi 8\sqrt{2})m_e^{\ast \frac{3}{2}}}{h^3}{\int }_{E_c}^{\infty }\sqrt{E-E_c}\exp [-\frac{E-E_F}{kT}]dE\\ & =N_c\exp [-\frac{E_c-E_F}{kT}]\end{array}$$

这里有

$$N_c=2(\frac{2\pi m_e^{\ast }kT}{h^2}{)}^{\frac{3}{2}}$$

这里电子的有效质量 $m_e^{\ast }$ 值是 $9.1\times 10^{-31}\mathrm{kg}$。 $N_c$ 被称为导带有效态密度 (Effective Density of States in the Conduction Band)，表示在导带中可用的电子态的数量。

可以对价带中的空穴密度进行类似的计算。将价带中的态密度 $g_{vb}(E)$ 和费米函数 $f(E)$ 与 1 的差相乘并积分，得到空穴浓度 $p$：

$$p={\int }_0^{E_v}{p}_{E}dE={\int }_0^{E_v}{g}_{vb}(E)[1-f(E)]dE$$

因为电子缺失的概率是 $p$，同时也是单位能量中的空穴浓度。而电子出现的概率是 $f(E)$，所以 $1-f(E)$ 就是空穴出现的概率。

假定 $E_F$ 比 $E_v$ 高几个 $kT$，可以得到近似解：

$$p=N_v\exp [-\frac{E_F-E_v}{kT}]$$

这里有

$$N_v=2(\frac{2\pi m_h^{\ast }kT}{h^2}{)}^{\frac{3}{2}}$$

$N_v$ 被称为价带有效态密度 (Effective Density of States in the Valence Band)，表示在价带中可用的空穴态的数量。 $m_h^{\ast }$ 是空穴的有效质量。

使用空穴密度和电子密度的表达式，计算出本征载流子浓度 (Intrinsic Carrier Concentration)：

$$\begin{array}{rl}np& =n_i^2\\ & =N_c\exp [-\frac{E_c-E_F}{kT}]\times N_v\exp [-\frac{E_F-E_v}{kT}]\\ & =N_c{N}_v\exp [-\frac{E_c-E_v}{kT}]\\ & =N_c{N}_v\exp (-\frac{E_g}{kT})\end{array}$$

本征半导体是一种纯净的半导体晶体，电子和空穴对浓度相同，几乎不含杂质，费米能级位于禁带中间。此处的 $n_i$ 就是本征载流子浓度。

已严肃被绕晕

课上练习：