Lecture 02 - Fundamental Concepts in Optimization

1. Exam Focus（真题对齐）

High-frequency (A 档)

• Engineering problem formulation (6-step procedure)
  • 2022-2023 Q2(a): formulate antenna design into an optimization problem
  • 2023-2024 Q1(a): list objectives (if any) and constraints (if any) for filter design
  • 2024-2025 Q2(a): define decision variables (how many? type? range?) for a defense optimization tool
• Objectives vs constraints; feasible/infeasible; comparing solutions (constraint violations)
  • 2022-2023 Q1(d): concepts of objectives/constraints/feasible solutions
  • 2023-2024 Q1(a)(b): objectives/constraints + integrate them (integration handled later, but classification is from this lecture)
  • 2024-2025 Q1(a)(b): number of objectives/constraints; integrate constraints into a single function
• Multi-objective optimization: domination, non-dominated, PF/PS (PF = F(PS)); compare Pareto fronts
  • 2022-2023 Q1(e): Pareto optimal / PS vs PF / non-dominated
  • 2023-2024 Q2(a)(b): choose multiobjective vs constrained single objective; compare two PFs
  • 2024-2025 Q2(b): compare PFs (minimization)
• Decision-variable representation (continuous / binary / permutation) + search space
  • 2024-2025 Q2(a): “m or n variables?”, “continuous/binary/permutation?”, “range?”
  • 2023-2024 Q2(c): delivery plan solutions are permutations (representation is prerequisite)

Medium (B 档)

• Global vs local optimum; local vs global optimization; neighborhood
  • 2022-2023 Q1(b): hill climbing is local search (ties to local optimum & neighborhood)
• Unimodal vs multimodal
  • 2022-2023 Q1(h): multimodal means >1 local optimum

Low (C 档)

• Engineering case study details (antenna array, network slicing, etc.)
  • Usually not directly examined; used as modeling examples.

Scoring checklist（本节课拿分点清单，可直接背）

• Can write the generic optimization form: variables + objective(s) + constraint(s) + search space
• Can apply the 6-step procedure to translate text specs → math model
• Can correctly distinguish objective vs constraint
• Can rank solutions: feasible（可行解） > infeasible（不可行解）; infeasible vs infeasible uses violation
• Can define domination (min/max), identify non-dominated set, and explain PF/PS (+ PF=F(PS))
• Can compare two Pareto fronts using convergence + diversity/coverage
• Can state decision-variable representation (continuous/binary/permutation) and ranges

---

2. Key Concepts（知识点）

A 档（必会）

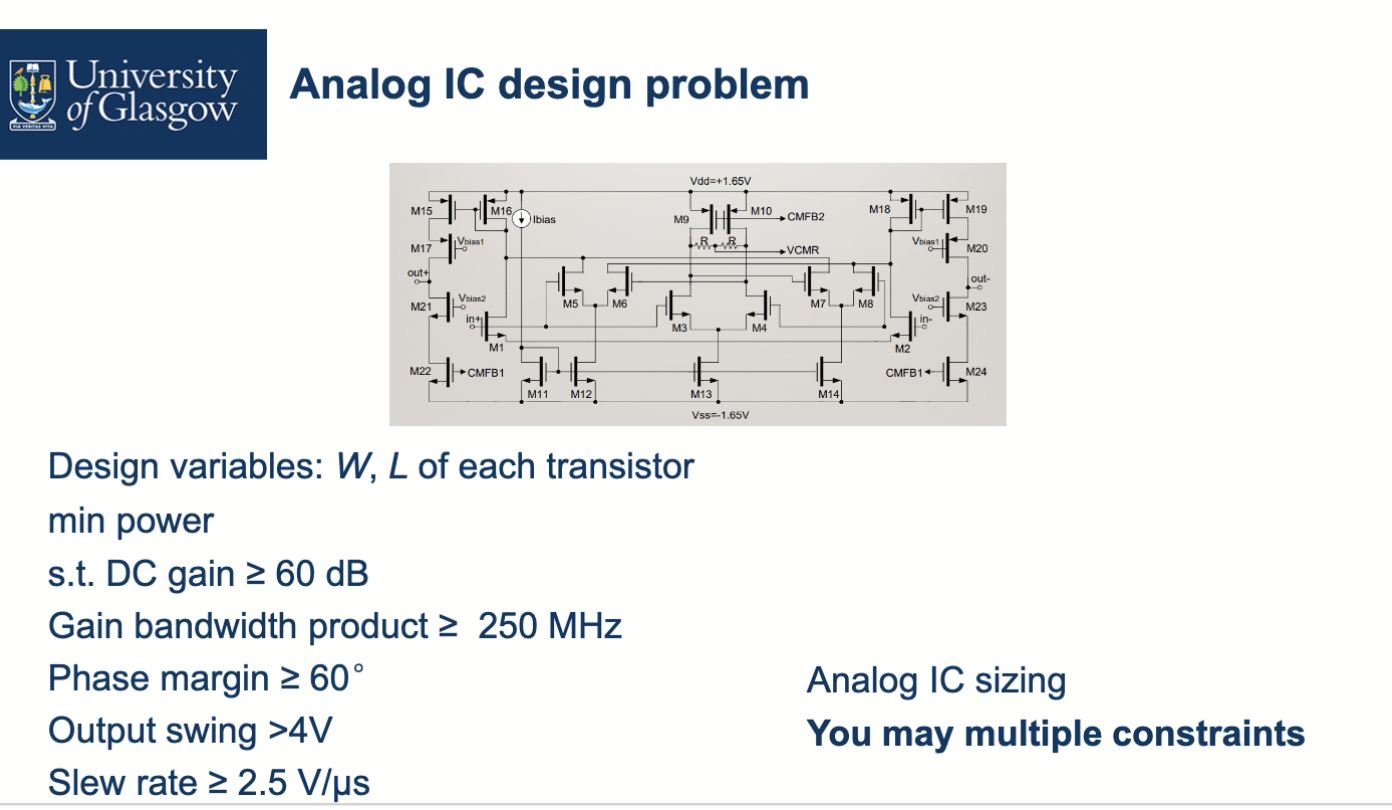
(A1) 6-step procedure: formulate engineering problems into optimization problems

1. Identify requirements
2. Classify requirements to objectives and constraints
3. Identify decision variables and their properties (type: continuous（连续）/binary（二项分布）/permutation（排列）/...)
4. Identify search space (ranges / feasible domain)
5. Identify if there is a starting point
6. Identify how to obtain objective and constraint values (simulation/measurement)

(A2) Objectives vs constraints; feasible space; comparing solutions

• Decision variables : (X)
• Objective : optimize (min/max)
• Constraints : must satisfy (feasible/infeasible)
• Feasible space : set of all solutions satisfying constraints
• Comparing solutions (PPT rule)
  1. Two feasible: compare objective
  2. Feasible vs infeasible: feasible is better
  3. Two infeasible: compare constraint violations (smaller violation is better)

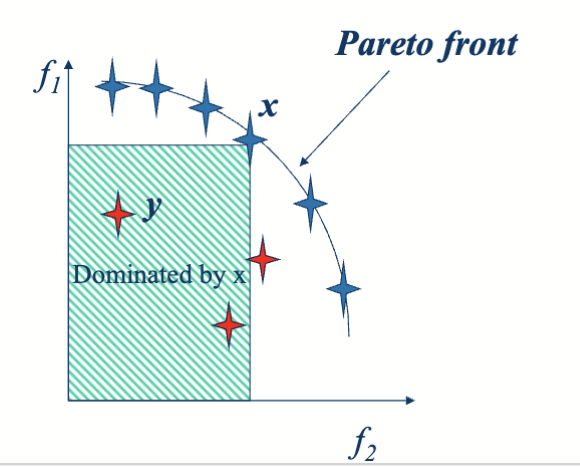
(A3) Multi-objective optimization; domination; Pareto front / Pareto set

• Multiobjective form:$$max/min{f}_1(\mathbf{x}),max/min{f}_2(\mathbf{x}),\mathbf{x}\in D$$
• Domination (example for maximization; for minimization flip the inequalities):

$$\mathbf{x}\prec \mathbf{y}⟺(\mathrm{\forall }k,f_k(\mathbf{x})\ge f_k(\mathbf{y}))\wedge (\mathrm{\exists }k,f_k(\mathbf{x})>f_k(\mathbf{y}))$$

• Pareto-optimal (non-dominated): not dominated by any other solution
• Pareto set (PS): Pareto-optimal solutions in decision space
• Pareto front (PF): objective vectors of PS in objective space$$PF=F(PS)$$

(A4) Decision-variable representation + search space

• Binary : $x_i\in \{0,1\}$ (feature selection / knapsack selection)
• Permutation : $\mathbf{p}$ is a permutation of $\{1,\dots ,n\}$ (TSP/QAP)
• Continuous : $\mathbf{x}\in {\mathbb{R}}^n$, each with bounds $[l_i,u_i]$

---

B 档（可能考）

(B1) Global vs local optimum; neighborhood

• Global optimum (max case):$$x^{\ast }\text{ is global optimal }⟺\mathrm{\forall }x\in \mathrm{\Omega },f(x^{\ast })\ge f(x)$$
• Neighborhood $\mathcal{N}(x)$: points considered "close" (definition depends on problem: Euclidean/Hamming/swap)
• Local optimum: best within (\mathcal{N}(x))

(Old-note image preserved)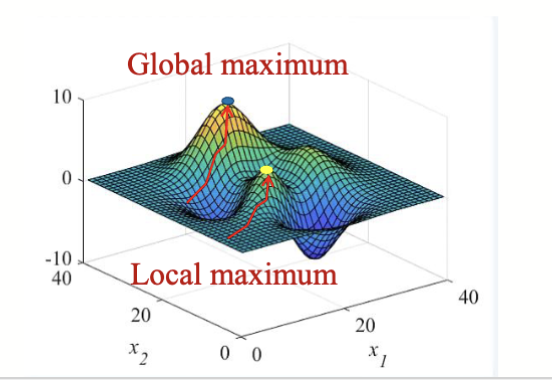

(B2) Unimodal vs multimodal

• Unimodal: single optimum basin
• Multimodal: multiple local optima (local search can get stuck)

---

C 档（低频）

• Case-study-specific domain details (antenna/network slicing/radar features): know they are examples of modeling, not memorization targets.

---

3. Must-know Formulas / Algorithms（公式/算法模板）

3.1 Constrained optimization template（可抄）

$$\begin{array}{rl}min/max& f(\mathbf{x})\\ \mathrm{s}.\mathrm{t}.& g_i(\mathbf{x})\ge 0,i=1,\dots m;\\ & h_j(\mathbf{x})=0,j=1,\dots ,r\\ & \mathbf{x}\in \mathrm{\Omega }\end{array}$$

3.2 Comparing solutions in constrained optimization（PPT rule）

1. Feasible vs feasible: compare objective value
2. Feasible vs infeasible: feasible is always better
3. Infeasible vs infeasible: compare constraint violation (smaller is better)

(Optional violation scalar you can write if needed)

$$v(\mathbf{x})=\sum _{i}max(0,-g_i(\mathbf{x}))$$

3.3 Domination & Pareto (2-objective)

• (Max case) domination:$$\mathbf{x}\prec \mathbf{y}⟺(\mathrm{\forall }k,f_k(\mathbf{x})\ge f_k(\mathbf{y}))\wedge (\mathrm{\exists }k,f_k(\mathbf{x})>f_k(\mathbf{y}))$$
• PF/PS relation:$$PF=F(PS)$$

3.4 6-step procedure（流程编号，答题直接写）

1. Requirements list
2. Objective(s) + constraint(s)
3. Decision variables + type
4. Search space/ranges
5. Starting point?
6. How to compute objective/constraints (simulation/measurement)

---

4. Worked Examples（例题与解答）

Note: These are “exam-style” and aligned to past papers’ wording.

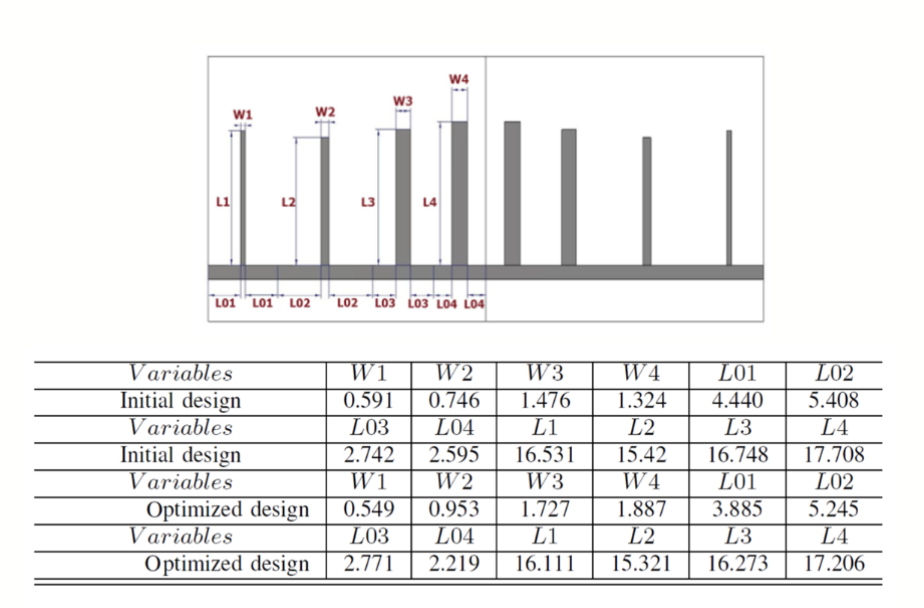
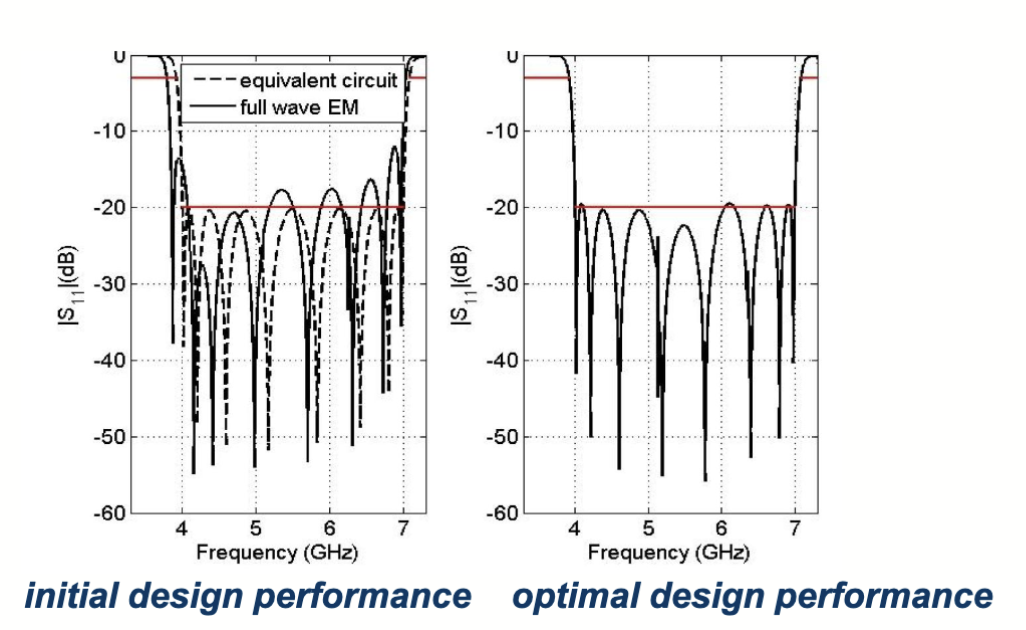
A1 Example 1 — Filter design (formulation)

Problem
Given passband and two stopbands specs with S11(dB), formulate min problem with objective & constraints, define $\mathbf{x}\in {\mathbb{R}}^{12}$, search space $\mathrm{\Omega }$, and evaluation method.

Solution :

• Variables: $\mathbf{x}=(x_1,\dots ,x_{12})\in {\mathbb{R}}^{12}$
• Objective:$$minf(\mathbf{x})=\underset{f\in [4,7]}{max}|S11(\mathbf{x},f)|$$
• Constraints:$$\begin{array}{rl}& \underset{f\in [3.3,3.92]}{min}|S11(\mathbf{x},f)|\ge -3,\\ & \underset{f\in [7.08,7.3]}{min}|S11(\mathbf{x},f)|\ge -3\end{array}$$
• Search space:$$\mathbf{x}\in \mathrm{\Omega }=\prod _{i=1}^{12}[l_i,u_i]$$
• Evaluation: EM simulation → extract S-parameters → take max/min over bands

Final Answer
Write the above min/s.t. + $\mathbf{x}\in \mathrm{\Omega }$ + simulation-based evaluation.

---

A1 Example 2 — Antenna design (formulation)

Problem
Band 1.1–1.7 GHz: require $max|S11|\le -14$ and $maxAR\le 3$. Minimize size $S(\mathbf{x})$.

Solution :

$$\begin{array}{rl}min& S(\mathbf{x})\\ \text{s.t. }& \underset{band}{max}|S11(\mathbf{x})|\le -14,\\ & \underset{band}{max}AR(\mathbf{x})\le 3,\mathbf{x}\in \mathrm{\Omega }\end{array}$$

Final Answer
Objective = size; constraints = two band-max specs; $\mathbf{x}$ continuous with bounds; simulation gives curves then max over band.

---

A2 Example 1 — Compare solutions (feasible > infeasible)

Problem
$minf(x)=-(x-1{)}^2$, s.t. $g(x)=x-1.5\ge 0$. Candidates: 0.5, 1, 1.5, 2.

Solution
Compute $g(x)$: only 1.5 and 2 are feasible. Compare feasible by objective:
$f(1.5)=-0.25,f(2)=-1\Rightarrow 2$ is best.

Final Answer
Best solution: $x=2$.

---

A2 Example 2 — Rank by constraint violations

Problem
Min problem with $g_1,g_2\ge 0$.
A: $g_2<0$, B: feasible, C: both <0. Rank.

Solution
Feasible beats infeasible ⇒ B best.
Among infeasible, compare violation sum $v(\mathbf{x})=\sum max(0,-g_i)$: smaller $v$ is better ⇒ A better than C.

Final Answer
B > A > C.

---

A3 Example 1 — Find PF (minimization)

Problem
Given several (f1,f2) points, find non-dominated set.

Solution
Use min-domination: $x\prec y$ if $f_1(x)\le f_1(y)$ and $f_2(x)\le f_2(y)$ and one strict. Remove dominated points.

Final Answer
Remaining points are PF.

---

A3 Example 2 — Compare two PFs (8-mark style)

Problem
Two algorithms produce two PFs (min). Compare.

Solution :

• Convergence: closer to left-bottom is better
• Diversity: wider coverage + more uniform spacing is better
  Write 3–5 sentences using these keywords.

Final Answer
A complete comment must mention both convergence and diversity/coverage.

---

A4 Example 1 — Representation & ranges

Problem
Feature selection / TSP / network slicing: specify variable type and range.

Solution :

• Feature selection: $x_i\in \{0,1\}$
• TSP: permutation of $\{1,\dots ,n\}$
• Network slicing: continuous $\beta \in [0,1]$

Final Answer
State variable count (n), type, and range.

---

A4 Example 2 — Swap neighborhood (permutation)

Problem
For $x=(2,3,4,1)$, list neighbors by one swap.

Solution
There are $(\genfrac{}{}{0ex}{}{4}{2})=6$ swaps; list all 6 resulting permutations.

Final Answer
(3,2,4,1), (4,3,2,1), (1,3,4,2), (2,4,3,1), (2,1,4,3), (2,3,1,4)

---

5. Common Mistakes（易错点，扣分点 ≥10，按重要性排序）

1. 把“必须满足的规格”误写成目标（却不说明多目标/不写处理方式）
2. 忘写搜索空间 $\mathbf{x}\in \mathrm{\Omega }$ 或变量范围（缺“可优化的域”）
3. 频段指标是向量却没写“max/min over band”（缺“向量 → 标量聚合”）
4. 可行/不可行比较规则写反（应：feasible > infeasible）
5. 两个不可行解不比违约程度，反而比目标值（规则错）
6. Domination 忘了“至少一项严格更好”
7. min/max 方向搞反，导致 PF 全错
8. 把 Pareto set 当 Pareto front（PS 在决策空间，PF 在目标空间）
9. PF 比较只写“算法 2 更好”不给依据（必须写 convergence + diversity/coverage）
10. TSP/QAP 误用二进制/实数表示且不加可行性约束（表示法错误）
11. 邻域定义混乱（swap vs adjacent swap；欧氏 vs Hamming）
12. 把 multimodal 误解成“多变量/多目标”，而不是“多个局部最优”

---

6. Quick Review（考前 10 分钟速记）

6.1 必背模板（3 行写完建模）

$$\begin{array}{rl}min/max& f(\mathbf{x})\\ \text{s.t.}& g_i(\mathbf{x})\ge 0,\mathbf{x}\in \mathrm{\Omega }\end{array}$$

• 先写：变量（个数/类型/范围）
• 再写：目标（越大越好 or 越小越好 + 频段用 max/min 聚合）
• 最后写：约束（必须满足的规格）

6.2 6-step procedure（背到能默写）

1. Requirements
2. Objective(s) + constraint(s)
3. Variables + type
4. Search space/ranges
5. Starting point?
6. Evaluation method (simulation/measurement)

6.3 Constrained ranking（PPT 原规则一句话）

• feasible > infeasible；feasible 之间比目标；infeasible 之间比违约

6.4 Pareto（两句拿满分）

• domination：所有目标不差 + 至少一个更好
• PF：所有非支配点集合；PS 在决策空间，PF 在目标空间，且 $PF=F(PS)$

6.5 PF 对比（8 分关键词）

• Convergence（更靠近理想点） + Diversity/Coverage（覆盖更宽、更均匀、不扎堆）