Lec.3 遗传算法
介绍
遗传算法 (Genetic Algorithm, GA) 是一种模拟自然选择和遗传机制的优化算法。它通过模拟生物进化过程中的选择、交叉和变异等操作,逐步改进解的质量,以找到问题的最优解或近似最优解。GA 用户用于优化问题,通常易于实施,能够求解复杂的优化问题,在计算机算力逐渐上升的趋势中,GA 的应用越来越广泛。
这种算法属于计算智能 (Computational Intelligence) 的范畴(如神经网络、进化计算),从自然界中获取解决问题的方案的思路。从自然界中的生物进化,我们可以提取出这样的特征
- 个体 (Individual)
- 问题的一个解
- 用染色体 (Chromosome) 来表示
- 种群 (Population)
- 一些个体的集合
- 选择 (Selection):适者生存
- 一个个体的性能越好,就更可能成为亲代,产生下一代
- 交叉 (Crossover):基因重组
- 子代的染色体由它的两个亲代的染色体组合而成
- 变异 (Mutation):基因突变
- 个体的染色体在某些位置上发生随机变化
算法流程
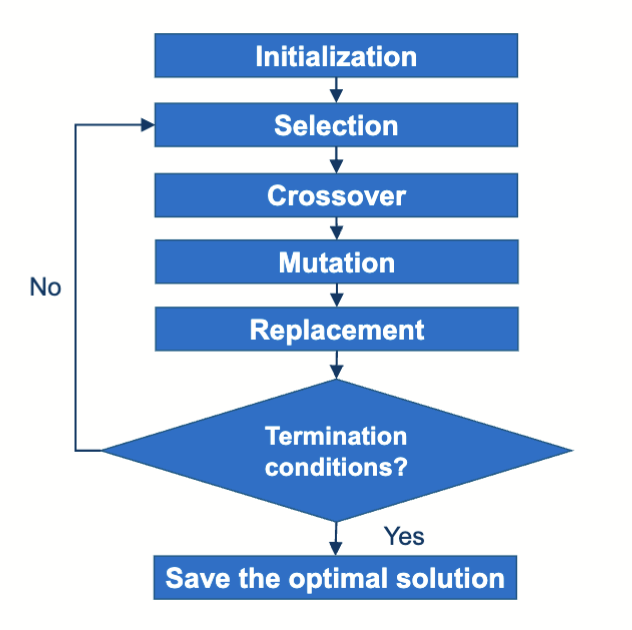
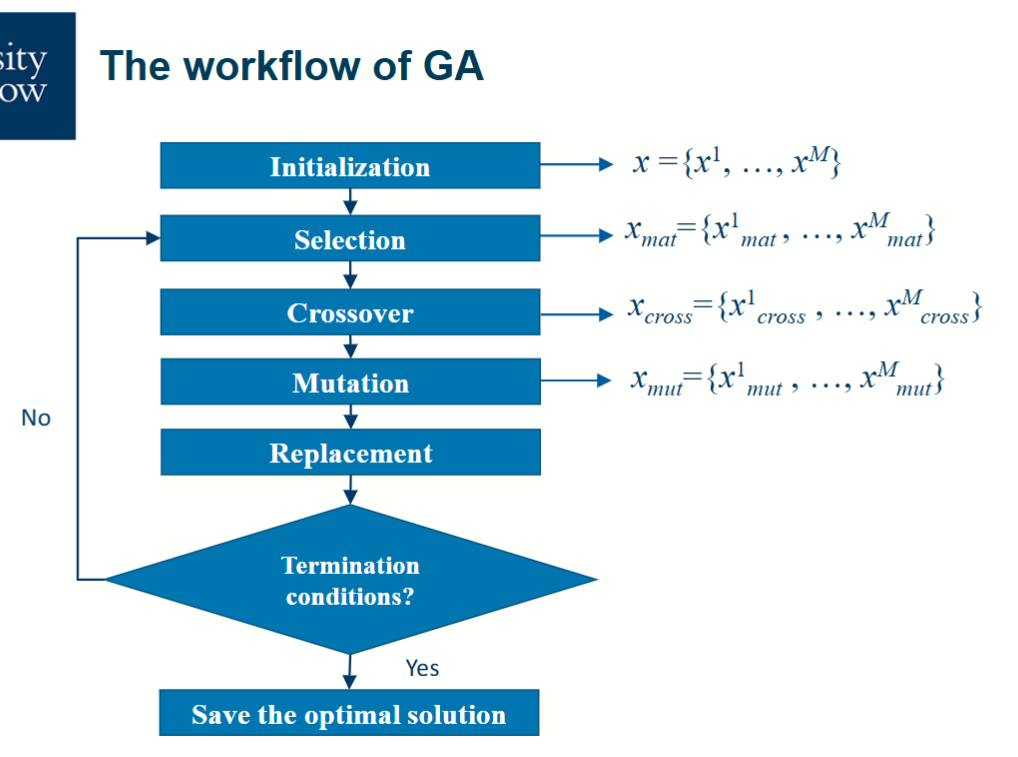
进行遗传算法的过程,就是模拟生物进化的过程。
- 首先,有一个种群
- 经过选择之后形成交配池 (Mating Pool)
- 亲代发生交叉和变异后形成新的种群
- 用新的种群替代原本的种群,重复以上操作
- 如果到达了停止条件,则结束优化过程,输出结果
首先需要考虑的是如何表示一个个体或者一组解,以满足我们需要后续操作的特质,如交换、变异等。常见的编码方式有以下几种
- 二进制字符串 (Binary String)
- 整个字符串相当于个体,每一位相当于基因
- 可以通过二进制和十进制的转换来表示整数
- 实数编码 (Real-valued Encoding)
- 每个基因是一个实数,适合实值优化问题
- 排列编码 (Permutation Encoding)
- 每个个体是一个给定元素的某种排列
- 适合表示排列问题,如旅行商问题
- 整数编码 (Integer Encoding)
- 每个基因是一个整数,适合整数规划问题
初始化种群
初始化种群是遗传算法的第一步,通常是随机生成一组个体。需要关注的重要参数主要有两个:种群数量 (Population Size) 和初始化方法 (Initialization Method)。
种群数量影响算法的多样性和收敛速度,通常需要根据具体问题进行调整。初始化方法可以是完全随机生成,也可以结合一些启发式方法,以提高初始解的质量。
选择操作决定哪些个体可以进入交配池
选择操作模拟自然界中“适者生存”的过程。选择操作决定哪些个体可以进入交配池,同时更优秀的个体有更高的概率被选择。判定优秀与否的标准是适应度函数 (Fitness Function),它衡量个体的质量。
常见的选择操作有:
比例选择 (Proportional Selection)
根据个体的适应度值按比例选择
比如,对于优化问题
一个个体进入交配池的概率正比于它的适应度 (Fitness)
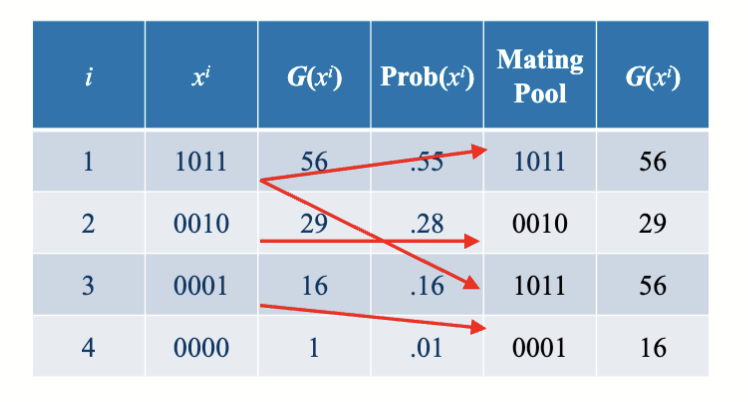
轮盘赌选择 (Roulette Wheel Selection)
将个体的适应度值映射到一个轮盘上,适应度越高的个体占据的区域越大,随机旋转轮盘选择个体
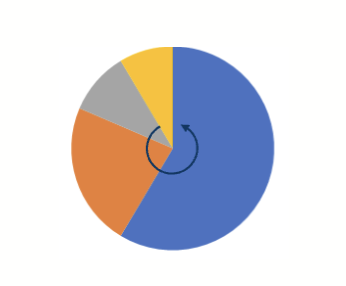
具体实现方法可以是生成一个随机数,根据随机数落在的区间选择对应的个体
锦标赛选择 (Tournament Selection)
随机选择若干个体,选出其中最优秀的个体
截断选择 (Truncation Selection)
选择适应度最高的一部分个体
| 最优性 (Optimality) | 多样性 (Diversity) | |
|---|---|---|
| 交配池数量 | 多于前代种群数量 | 少于前代种群数量 |
| 选择的作用 | 将搜索导向更有前途的部分 | 减少不同种类的数量 |
交叉 (Crossover) 和变异 (Mutation)
交叉和变异是生成新的种类的个体/解的方法。它们直接作用在个体上,通常在选择过程之后进行操作。在大多数情况下,交叉和变异的过程是和个体的适应度相互独立的。
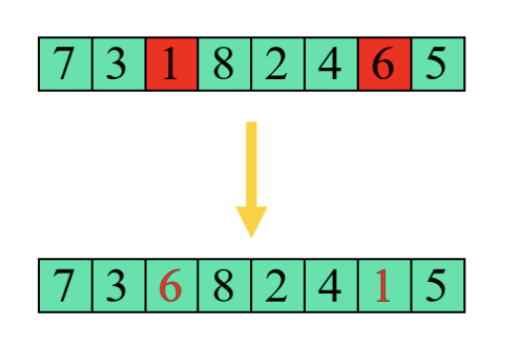
交叉操作指的是两个解的基因重组,交换各自染色体的一部分。其可以分为单点交叉 (Simple Crossover / One-Point Crossover)、K 点交叉 (K-Point Crossover) 等

- 单点交叉
- 从交配池中随机选择两个亲代
- 在染色体上随机选择一个交换位点
- 交换两个亲代在该位点之后的基因,生成两个子代
- K 点交叉
- 同理选择两个亲代
- 在染色体上随机选择 k 个交换位点
- 交叉这些位点之间的基因,生成两个子代
同样重要的是发生交叉的改率,成为交叉率 (Crossover Rate),其表示任意从交配池中选择的两个亲代发生交叉的改率,表示为
在程序实现上,通常是每个个体生成一个随机数
交叉操作可能会增加或者减小子代的平均适应度,但是会增加种群的多样性。在某些情况下,交叉操作不会生成新的个体,比如两个亲代完全相同,或者交换的位点在染色体的末尾,这种情况下选择和交叉操作无法解决问题。可以引入变异 (Mutation) 来增加种群的多样性。
对于每一个子代个体,有一个概率可以发生变异,记作
停止条件
如果停止条件没有满足,则持续进行选择、交叉和变异,生成新的种群,替代原本的种群,直到满足停止条件为止。常见的停止条件有:
- 达到最大迭代次数
- 种群收敛
- 达到预期的适应度水平
优缺点
- 优点
- GA 是一个通用的优化算法,和应用的领域无关
- 多种情况可以并行计算,提高计算效率
- 可以获得多种最优解,适合多目标优化问题
- 易于实现
- 缺点
- 可能不能获得全局最优解
- 参数选择对结果影响较大
- 计算资源消耗较大,计算不够快
使用遗传算法
要使用 GA 算法,需要先明确需要求解的问题和 GA 的各个参数的对应
- 求解的是什么问题
- 搜索空间是什么?有什么约束?
- 如何设计适应度函数?
- 如何表示一个解
- 如何初始化种群
- 如何合适的交叉和变异
- 如何选择作为亲代的个体
- 怎么用新的种群替代原本的种群
- 选择什么样的停止条件
如何表示一个解
表示一个解的方式有很多种,通常根据求解问题的特性来选择合适的编码方式,如搜索空间是连续的还是离散的,解的维度是多少等。
常见的编码方式有二进制编码、实数编码、排列编码和整数编码等。选择合适的编码方式可以影响算法的效率和效果。
怎么样初始化种群
初始化种群的目标是从搜索空间中均匀地采样,确保种群的多样性。常见的方法有随机生成和启发式生成。
- 对于二进制编码,可以随机生成二进制字符串,每一位是 0 或 1 的概率都是 0.5
- 对于实数编码,可以在每个维度上的取值范围内均匀随机采样
- 有一些其他的更试验性的方法
基于这样的采样方法,产生 N 个个体,组成初始种群。
如何合适的交叉或变异
变异
合适的变异操作需要保证
- 可以访问到搜索空间中的所有区域
- 变异的频率需要合适
- 变异后的结果应该是可行的解
- 如果对于特定问题有更合适的变异操作,可以优先使用
对于不同的编码方式,变异的操作也不同,常见的有
- 对于二进制编码,可以随机选择某一位进行翻转
- 对于实数编码,可以是对某一位加一个正态分布的随机数
- 对于排列,可以选择两个不同的位置进行交换
交叉
对于交叉,合适的交叉操作需要保证:
- 生成的子代同时继承两个亲代的特征
- 交叉后的结果应该是可行的解
- 如果对于特定问题有更合适的交叉操作,可以优先使用
对于不同的编码方式,交叉的操作也不同,常见的有
- 单点交叉
- 在染色体上随机选择一个交换位点
- 交换两个亲代在该位点之后的基因,生成两个子代
- 适用于二进制编码和实数编码
- K 点交叉
- 在染色体上随机选择 k 个交换位点
- 交叉这些位点之间的基因,生成两个子代
- 适用于二进制编码和实数编码
- m 亲本交叉
- 从 m 个亲本中选择基因,生成两个子代
- 适用于二进制编码和实数编码
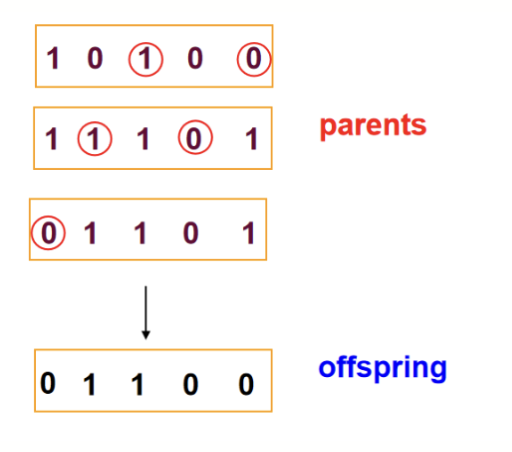
- 均匀交叉 (Uniform Crossover)
- 每个基因随机选择来自两个亲代中的一个
- 适用于二进制编码和实数编码
- 算术交叉 (Intermediate Crossover / Arithmetic Crossover)
- 对实数编码,生成子代为两个亲代的加权平均
是一个在 之间的随机数 取 0.5 时即为取平均值 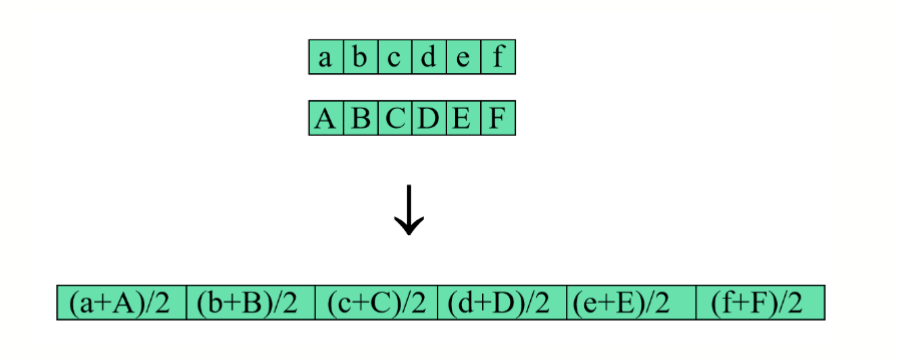
- 对实数编码,生成子代为两个亲代的加权平均
- 有序交叉 (Order Crossover, OX)
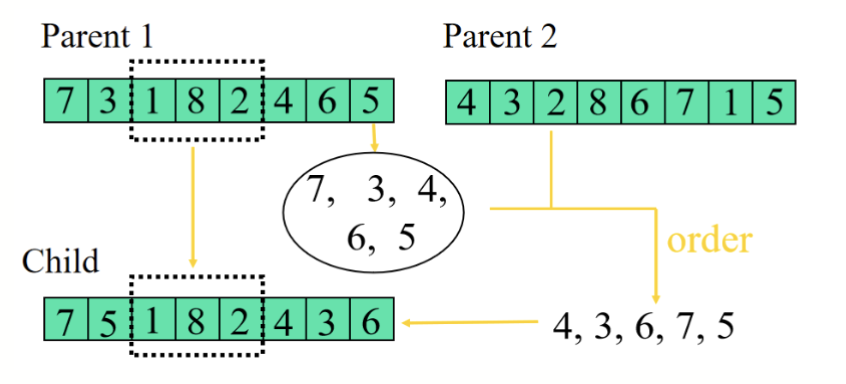
- 适用于排列编码
- 从一个亲本中选择一部分排列,复制到它的第一个子代中
- 把剩余的元素按照另一个亲本的顺序排序
- 从已有排列之后开始填充剩余的数字,遇到染色体尾时回绕
- 交换两个亲本角色,产生第二个子代
如何选择作为亲代的个体
更优秀的个体有更高的概率被选择作为亲代,但是弱小的个体也应该有一定的概率被选择,因为他们可能会产生更优秀的后代。
比例选择 (Proportional Selection)
使用比例选择的情况,用
指的是个体 的适应度 是种群的平均适应度 是交配池的容量
使用比例选择可能会引入一些问题
- 过早收敛 (Premature Convergence)
- 如果某个个体的适应度远高于其他个体,它可能会主导种群,导致多样性降低
- 在适应度相近时,选择压力较小,可能导致收敛速度变慢
为了解决这些问题,可以选择对适应度函数进行一些调整,但是仍要满足适应函数的要求:调整前后不会造成个体之间的相对顺序变化,同时,调整后的适应度值都为正数。一个典型的方法是使用线性映射
这样调整后就可以解决上述提到的问题:
- 出现一个个体的适应度远胜于其他个体时,取合适的
,可以增大其他个体的适应度,减小选择压力 - 出现所有个体的适应度都很接近时,取合适的
,可以增大选择压力,增大不同个体之间的相对差异
基于排名的选择 (Rank-Based Selection)
首先先计算出每个个体的适应度,根据适应度对每个个体进行排序,分配一个排名 (Rank),然后根据排名来决定个体被选择的概率。本质上也是一个对适应度函数的映射。
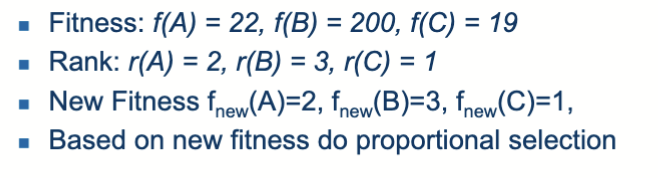
根据排名得到新的适应度值
锦标赛选择 (Tournament Selection)
随机选择
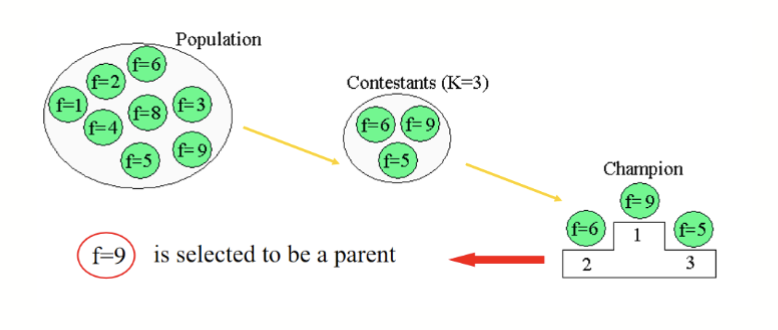
怎么用新的种群替代原本的种群
- 完全替代 (Full Replacement)
- 用新生成的种群完全替代原本的种群
- 简单易行,但可能会丢失一些优秀的个体
- 部分替代 (Partial Replacement)
- 幼崽和父母一起竞争进入下一代,更优秀的个体保留
选择什么样的停止条件
- 获得问题的最优解
- 根据 CPU 资源决定
- 最大迭代次数
- 根据用户耐心决定
- 达到预期的适应度水平
- 若干代内最优解没有变化
- Exploration vs. Exploitation
- Exploration:探索,寻找新的解空间
- 更多的探索会带来更多的多样性
- 不容易收敛
- 交叉主要起探索的作用
- Exploitation:利用,优化当前的解
- 更多的利用可能会陷入局部最优解
- 选择主要起利用的作用
- 需要在两者之间找到平衡
- Exploration:探索,寻找新的解空间
在 MATLAB 中使用遗传算法
性能测试
在正式使用一个算法解决问题之前,常常需要通过性能测试 (benchmark) 来评估一个算法的性能。为了评估算法的性能,我们会通常会使用已知答案的测试函数进行测试
- 测试函数包括许多不同特点
- 如可以是单模型、多模型、多变量等
- 用于评估算法在不同情况下的表现
- 已知测试函数的全局最优解
- 可以验证算法是否能够找到全局最优解
- 通常易于计算
- 便于快速评估算法的性能
- 有在已知的算法下的表现
- 可以与其他算法进行比较
通过性能测试,我们可以评估算法的收敛速度、稳定性和鲁棒性等性能指标,帮助我们选择合适的算法来解决实际问题。
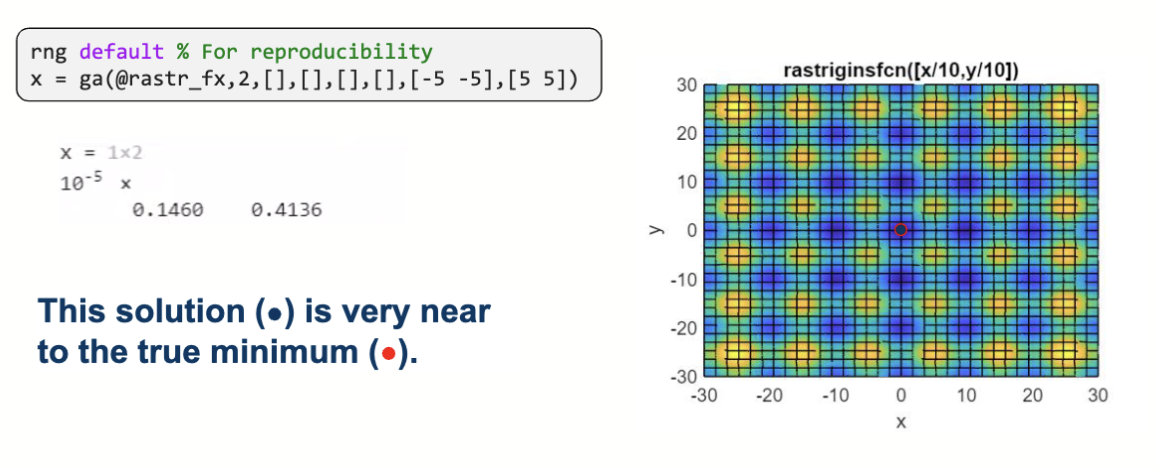
一个常见的测试函数是 Rastrigin 函数:
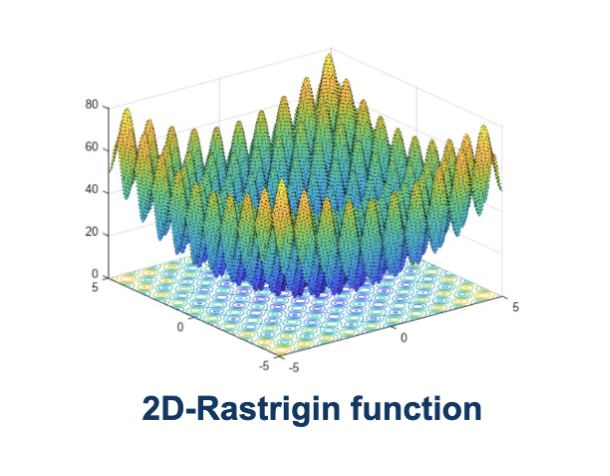
这个函数的特点是有多个局部最优解,但只有一个全局最优解,适合用来测试优化算法的性能。其全局最优解为
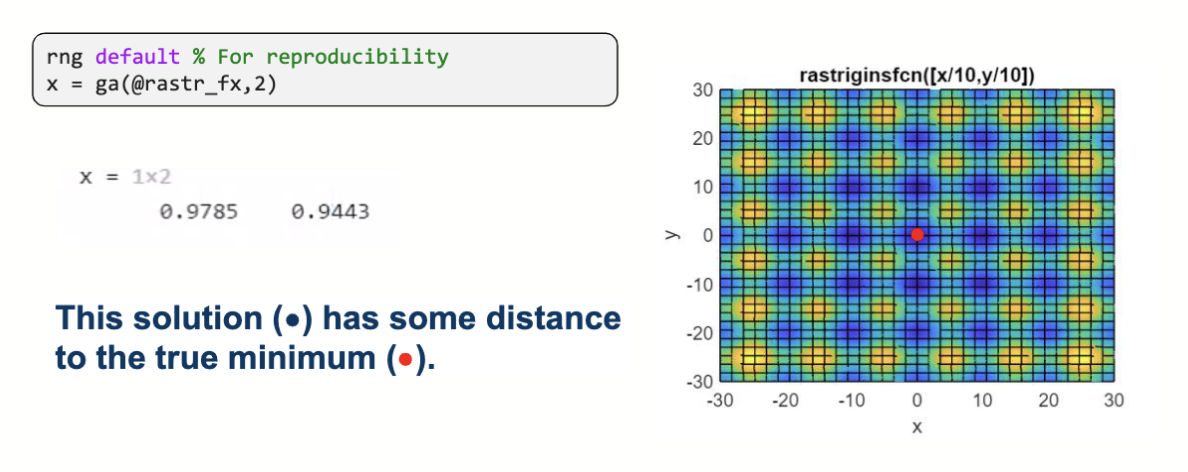
在只限定维度是 2 的情况下,得到的解和全局的最优解有一定距离。
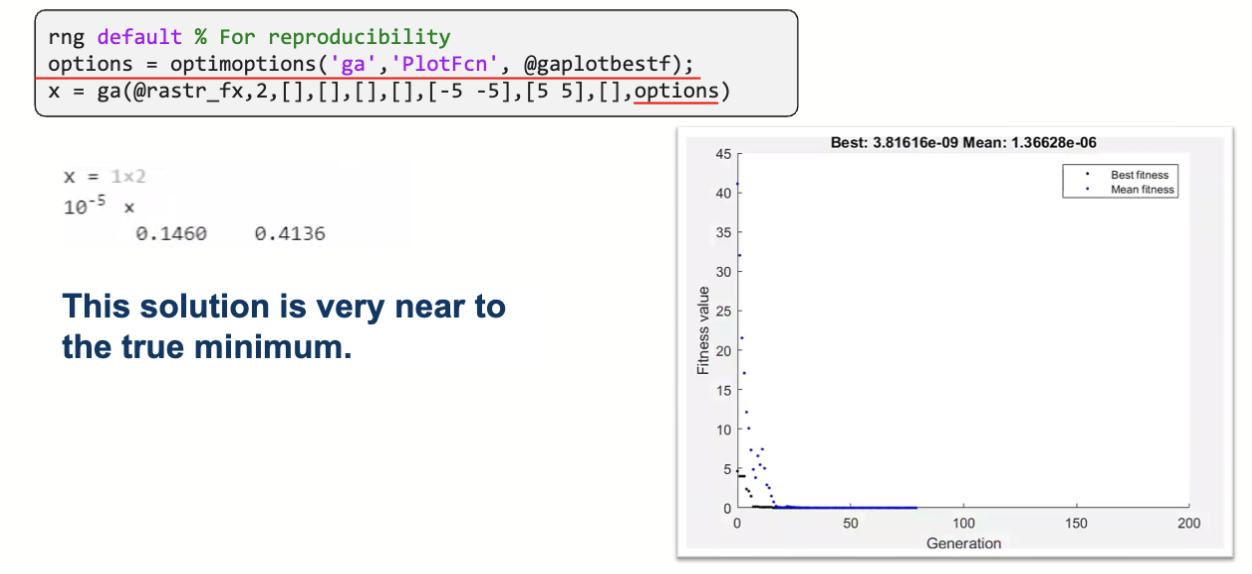
给每个维度添加了取值范围
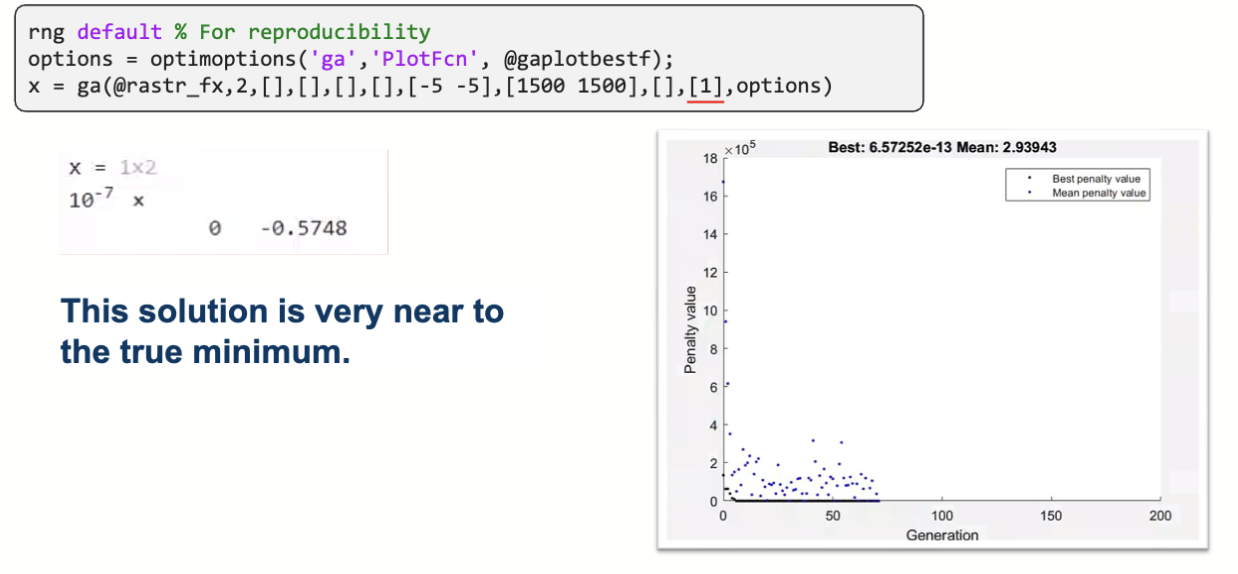
这里设置了 intcon 参数为 [1],表示第一个维度是整数类型。得到的解满足约束,且在全局最优解附近。
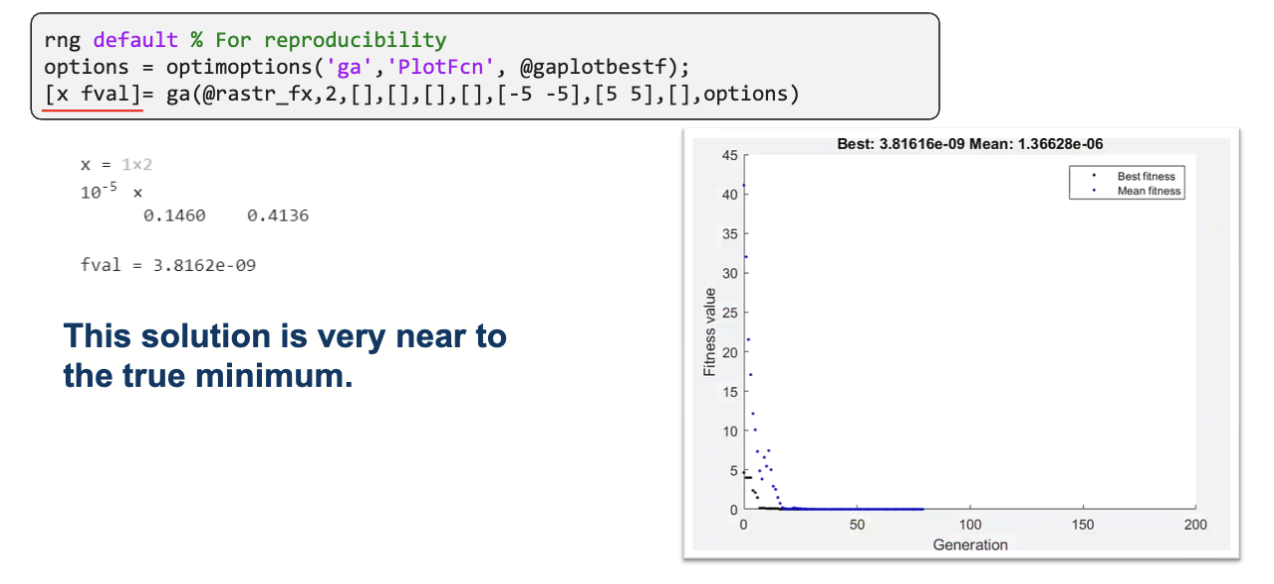
在获得局部最优解的变量取值时可以同时获得目标函数值。
偶极天线问题
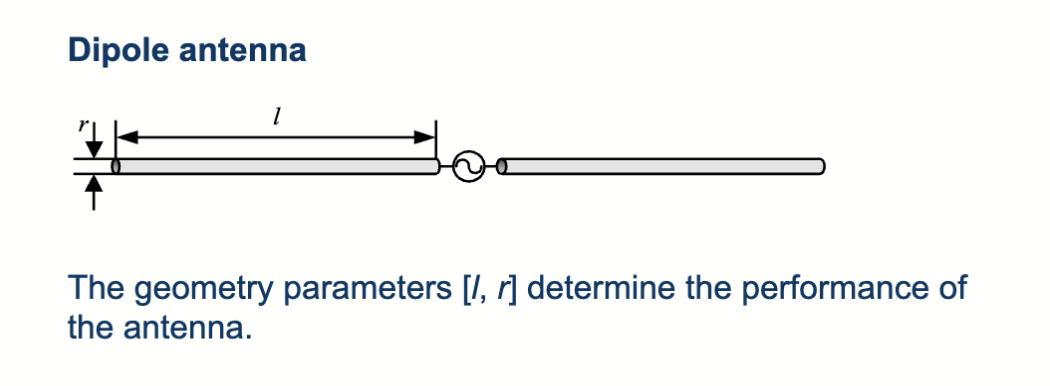
需要设计一个偶极天线,它的幅度
转换成 matlab 代码


经过 GA 算法优化后得到结果
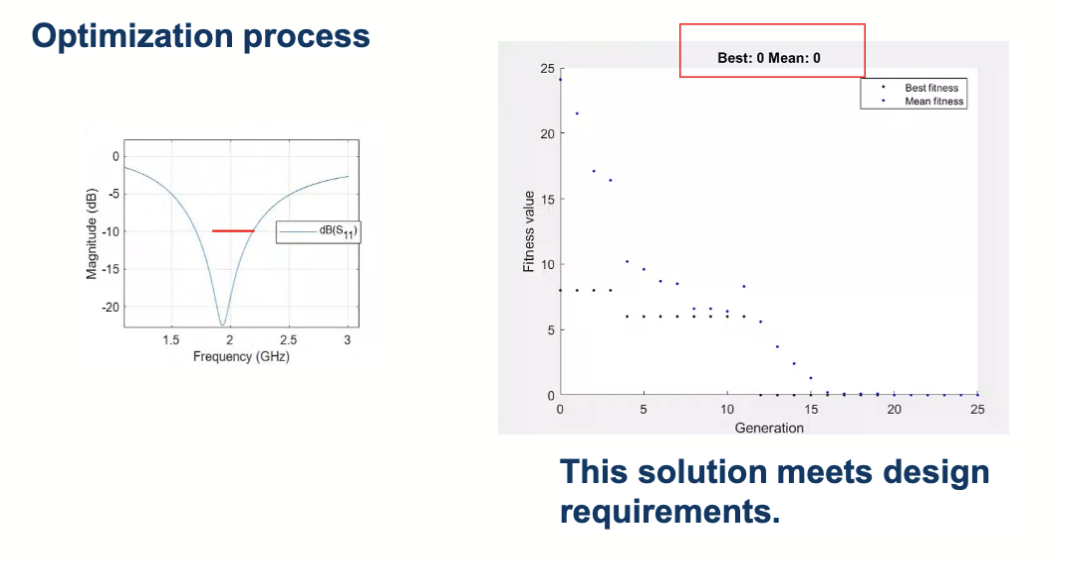
于是,得到了