Lec.5: Combinatorial Optimization (组合优化)

定义

组合优化指的是从一个有限的对象集中寻找最优解的问题。通常，这些对象集是离散的，并且问题通常涉及选择、排列或分配这些对象以最大化或最小化某个目标函数。

	组合优化 (CO)	实值优化 (RO)
目标	离散	连续
解空间	有限	无限
目标	在有限集合里寻找最好的组合或排列	寻找最好的解

常见的组合优化问题包括

• 背包问题 (Knapsack Problem)
• 旅行商问题 (Traveling Salesman Problem)

背包问题 (KP)

背包问题 (Knapsack Problem, KP) 指的是如何在一个给定了承载重量上限的背包中，选择物品以最大化总价值的问题。每个物品都有一个重量和一个价值，目标是选择一组物品，使得它们的总重量不超过背包的承载能力，同时总价值最大。

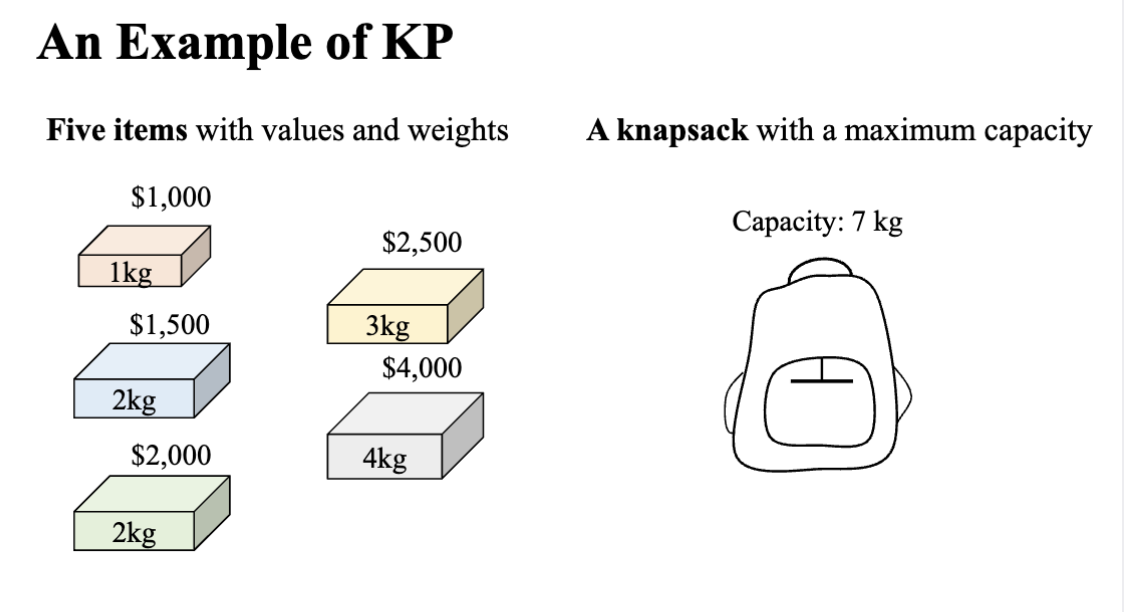
一个表示求解变量的方式是使用二进制编码，即对于 n 个物品，解是一个 n 维的二进制向量，其中每个元素表示对应物品是否被选择（1 表示选择，0 表示不选择）。

这里的情况，一共有 5 个物品可以选择，故使用一个五位的二进制数代表所有的选择情况，每一个二进制位对应一个物品，1 代表选择该物品，0 代表不选择该物品。

修复法 (Repairment Method)

为了方便求解，我们先计算出每个物品对应的单位重量价值，记作 $v2w$

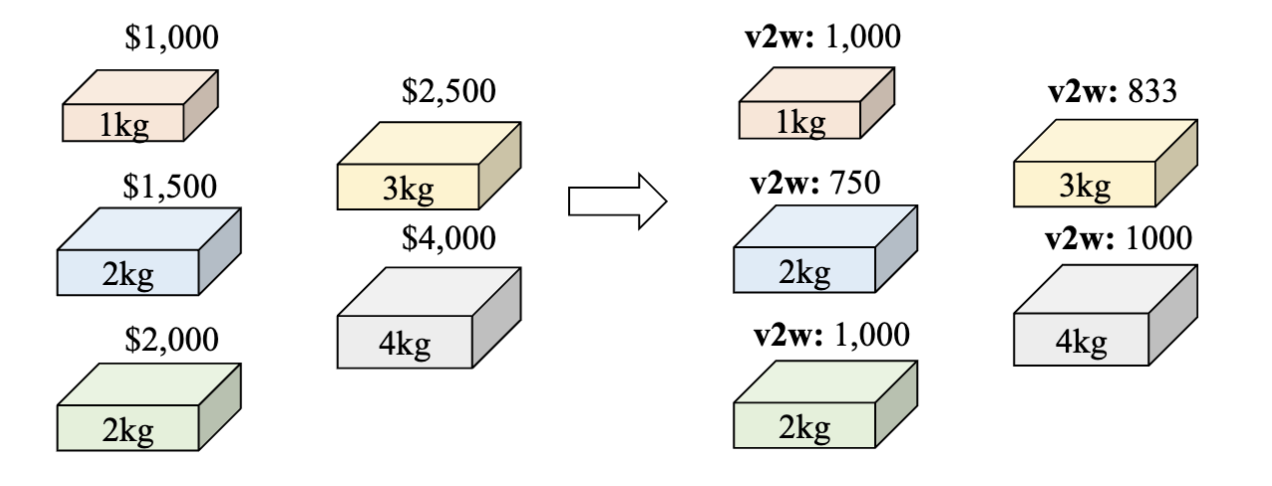
然后，我们使用单位重量价值而不是总价值对每个物品进行排序。比如

• 如果我们目前的二进制解是 01011， 总重量是 9 kg， 超过了 7 kg 的限制
• 通过单位重量价值排序，扔掉单位重量价值最低的物品，直到重量不超过限制

这样，在每一次迭代后都能产生新的保证可行的解。

惩罚函数法 (Penalty Function Method)

和 Lec.4 里提到的方法类似，我们把约束条件转化成惩罚项，加入到目标函数中，数学形式如下：

$$\begin{array}{rl}{f}_{new}(x)=& f(x)-p\cdot h(x)\\ \mathrm{where}& h(x)=\{\begin{array}{l}w(x)-c,\mathrm{if}w(x)>c\\ 0,\mathrm{otherwise}\end{array}\end{array}$$

• $f(x)$ 是原始的目标函数（总价值）
• $w(x)$ 是当前选择的物品的总重量
• $c$ 是背包的最大承载重量
• $p$ 是一个大的正数，表示惩罚的强度

确定 $p$ 的值的过程和 Lec.4 里提到的方法类似，都是按照 $p=\frac{50\tilde{f}}{ϵ}$ 的计算方法计算。

这里 $\tilde{f}$ 是一个对原始目标函数 $f(x)$ 的估计，取 $10000； $ϵ$ 是能够容忍的最大违反约束，这里取 1kg，计算出 $p=500000$。

使用上述方法，我们可以将背包问题转化为一个无约束优化问题，然后使用遗传算法或其他优化方法来求解。使用遗传算法求解得到这个问题的解是 10101，对应的最优目标函数是 $7k。

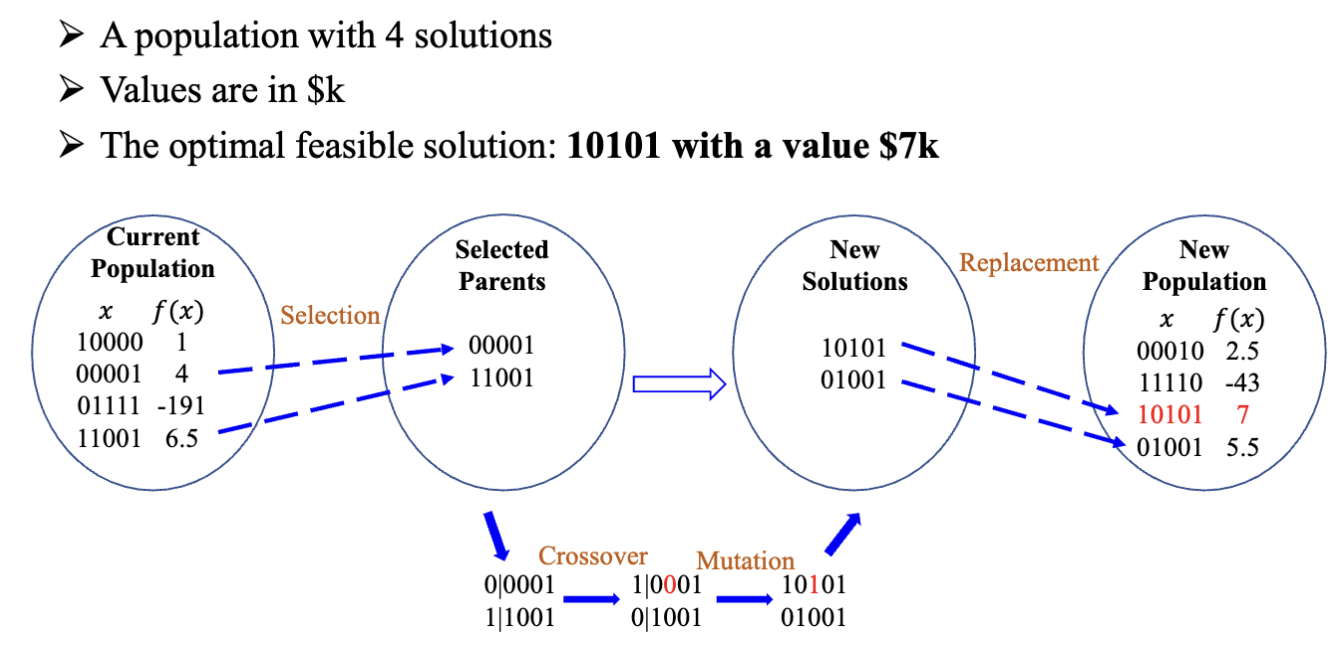
在 MATLAB 中求解背包问题

NOTE

在 MATLAB 中的对应实现在 Moodle 上的附加文件中，此处略过

这里使用了锦标赛选择 (Tournament Selection) 方法来选择交配池，在 Lec.3 里有介绍

旅行商问题 (TSP)

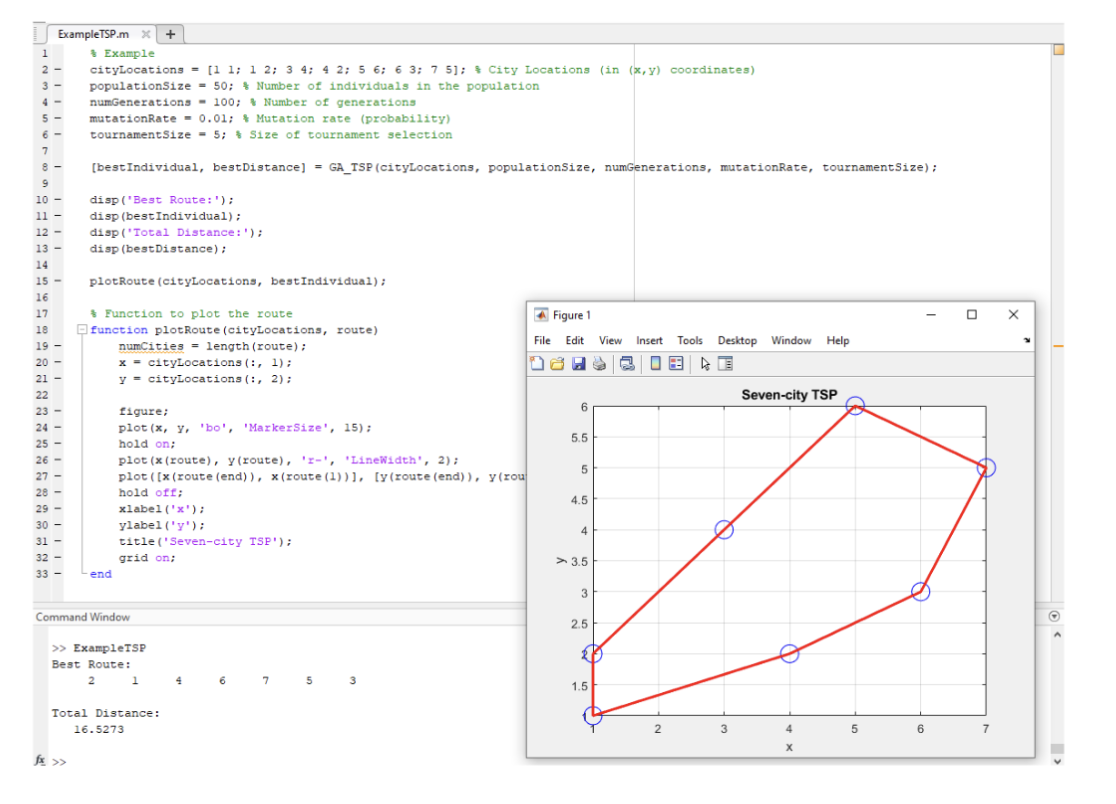
旅行商问题 (Traveling Salesman Problem, TSP) 是一个经典的组合优化问题，目标是在给定的一组城市中找到一条最短的巡回路径，使得每个城市恰好访问一次，并且最终返回到起始城市。

根据问题的性质，我们知道每个解应该是给定城市的排列————每个城市出现一次，不同的顺序代表访问城市的顺序。

按照这个编码，我们就像在 Lec.3 里提到的一样，我们不太可能使用普通的单点交叉进行交叉操作————它可能会破坏排列的性质，导致某些城市被访问多次，而其他城市则未被访问。

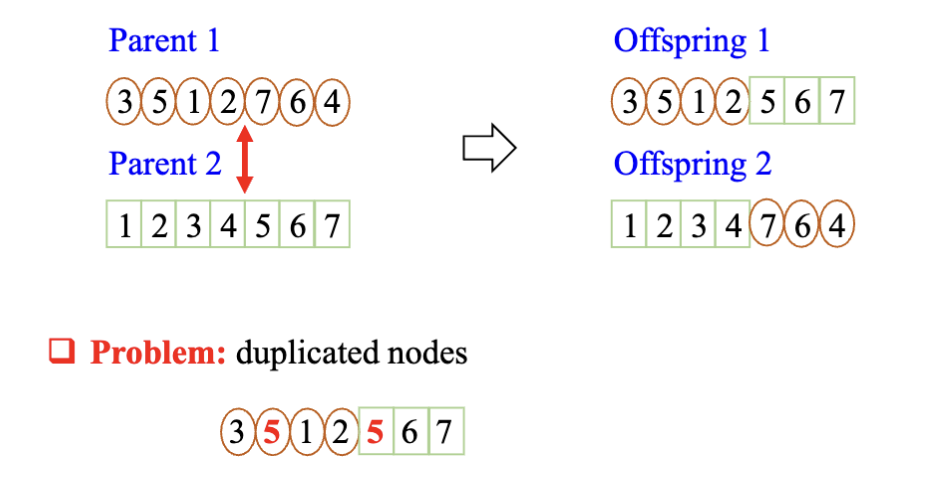
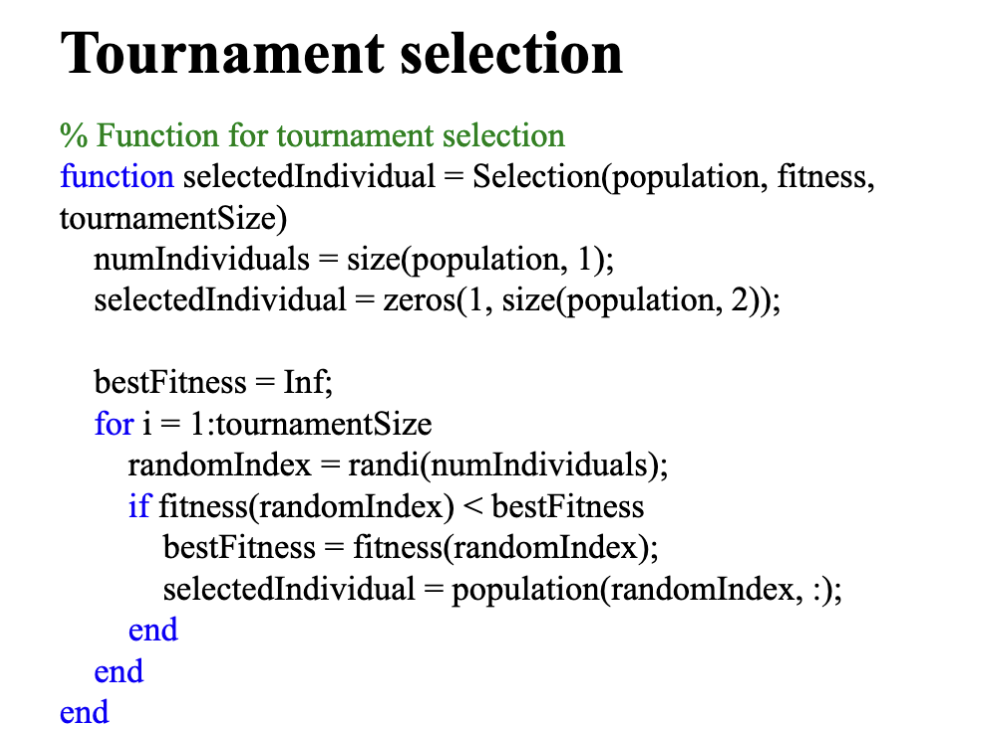
所以，这里使用有序交叉 (Order Crossover, OX)进行对应的交叉操作。

标准的 OX1 交叉是把提供顺序的亲本剩下的元素按顺序填充到子代切点之后，这里从第一个开始填充是一种简化版本的有序交叉。

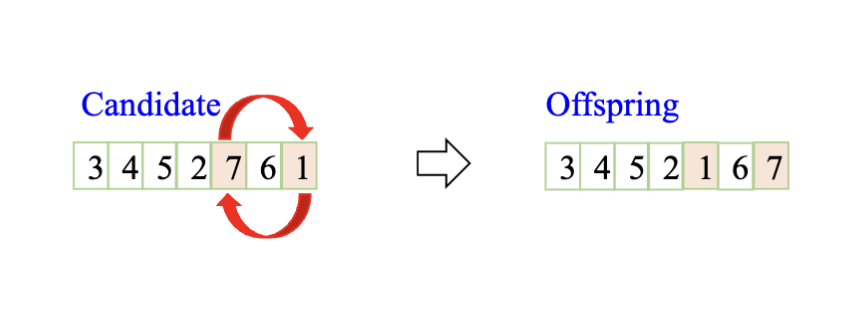
对于变异，则使用交换变异 (Swap Mutation)，即随机选择两个位置的城市并交换它们的位置。

接下来就是典型的遗传算法流程了。

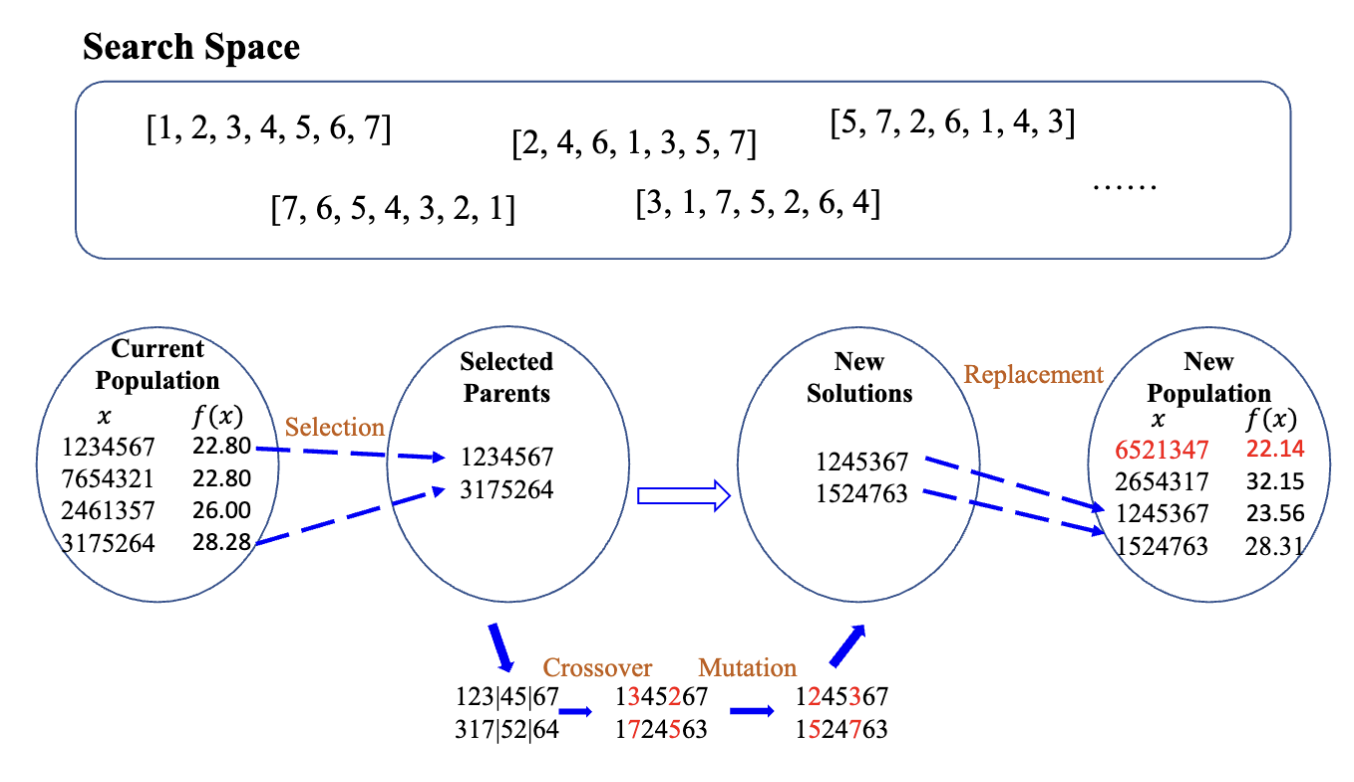
在 MATLAB 中求解旅行商问题

NOTE

在 MATLAB 中的对应实现在 Moodle 上的附加文件中，此处略过